Question

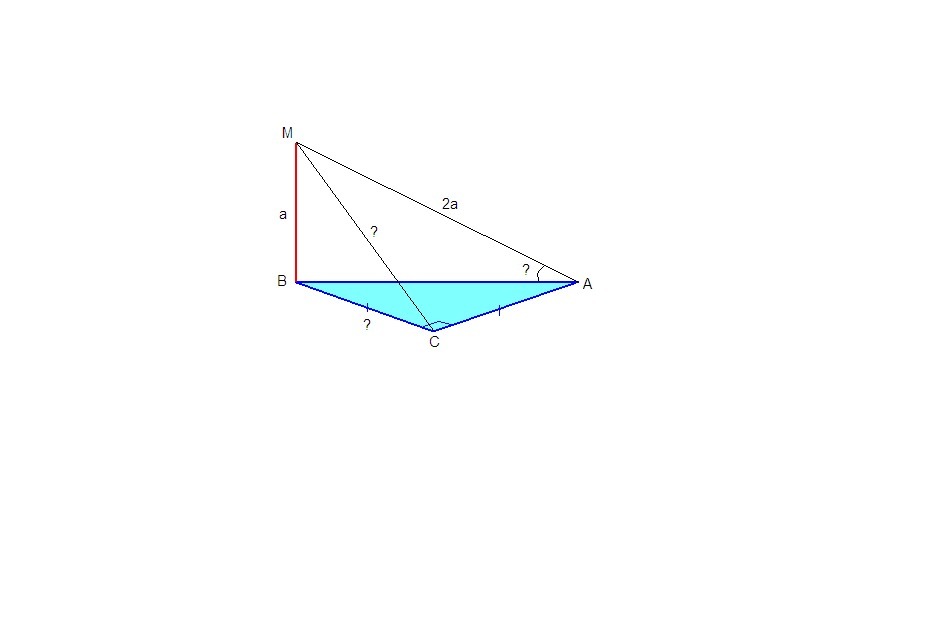
1. К плоскости прямоугольного треугольника АВС проведены перпендикуляр МВ и наклонные МА, МС. МА=2а, МВ = а.АСВ=90°, АС = ВС.

1) Вычислите угол между накло

нной МА и ее проекцией на плоскость треугольника АВС.

2) Вычислите длины наклонной МС и ее проекции.  

 

 

Answer 1

МВ - перпендикуляр к плоскости треугольника, значит
ВС - проекция наклонной МС,
ВА - проекция наклонной МА на плоскость треугольника,
надо найти МС, ВС и ∠МАВ.

ΔМВА: ∠МВА = 90°, катет МВ равен половине гипотенузы, значит
             ∠МАВ = 30°.
             cos30° = BA / MA
             √3/2 = BA / (2a)
             BA = 2a · √3/2 = a√3

ΔАВС равнобедренный, пусть АС = ВС = х, по теореме Пифагора:
x² + x² = BA²
2x² = 3a²
x² = 3a²/2
x = a√3 / √2 = a√6/2

BC = a√6/2

ΔMBC: по теореме Пифагора
              MC = √(MB² + BC²) = √(a² + 6a²/4) = √(10a²/4) = a√10/2