Question

задача 3.27

Диск радиуса R катится по прямой без проскальзывания . Найти радиус кривизны траектории точки A(x,y) диска (x != 0 , y != 0 ) .
ответ : $p = frac{ (x^{2} + y^{2})^{3/2} }{| x^{2} + y^{2} -yR|}$

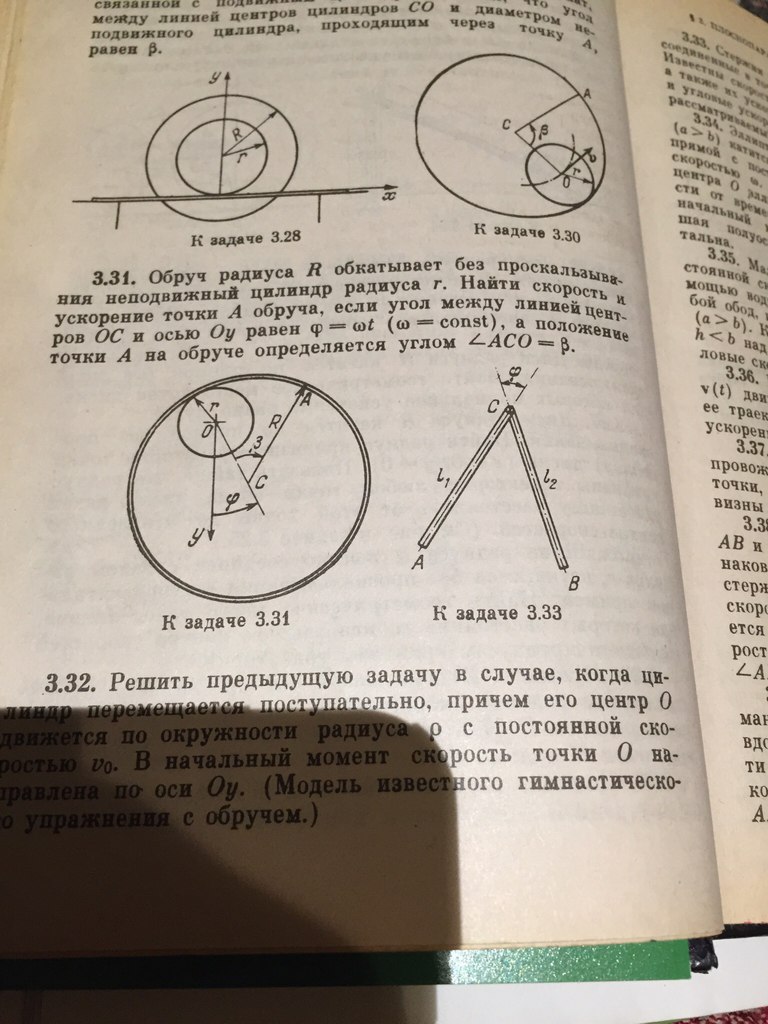
условие задача № 3.31 в приложении
$v_{a}=2(R-r)wsin( beta /2)$
$w_{a}= frac{w^{2}(R-r)}{R} sqrt{r^{2}+4R(R-r)sin^{2}( beta /2)}$

Answer 1

решение 1 задания во вложении

9464c5714e3e73a38390eb91638209b2.doc