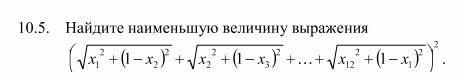Ответы
Ответ дал:
0
Обозначим хi= уi+0,5.
Когда раскроем скобки , получим сумму попарных произведений квадратных корней и сумму их квадратов. Сумма квадратов корней (у2+0,5)^2+(y2-0,5)^2+(y2+0,5)^2+.....+y1^2+y12^2
Эта сумма равна сумме квадратов уi + 1/4*12. . К этой сумме еще добавляется всегда положительная сумма попарных произведений радикалов. , Легко видеть, что минимум выражения достигается при уi=0, кроме 1-го и 12 -го- Значит минимум всего выражения достигается , когда все иксы равны 1/2, кроме 1 -го и 12 -го, которые равны 0.. Сам минимум равен (10 корней из 0,5 +1) в квадрате. Т.е. равен 51 +10*SQRT(2)
Ответ : наименьшее значение выражения 51 +10*SQRT(2). Достигается, когда все переменные равны 0,5 коме первой и последней, которые равны 0.
Когда раскроем скобки , получим сумму попарных произведений квадратных корней и сумму их квадратов. Сумма квадратов корней (у2+0,5)^2+(y2-0,5)^2+(y2+0,5)^2+.....+y1^2+y12^2
Эта сумма равна сумме квадратов уi + 1/4*12. . К этой сумме еще добавляется всегда положительная сумма попарных произведений радикалов. , Легко видеть, что минимум выражения достигается при уi=0, кроме 1-го и 12 -го- Значит минимум всего выражения достигается , когда все иксы равны 1/2, кроме 1 -го и 12 -го, которые равны 0.. Сам минимум равен (10 корней из 0,5 +1) в квадрате. Т.е. равен 51 +10*SQRT(2)
Ответ : наименьшее значение выражения 51 +10*SQRT(2). Достигается, когда все переменные равны 0,5 коме первой и последней, которые равны 0.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад