Question

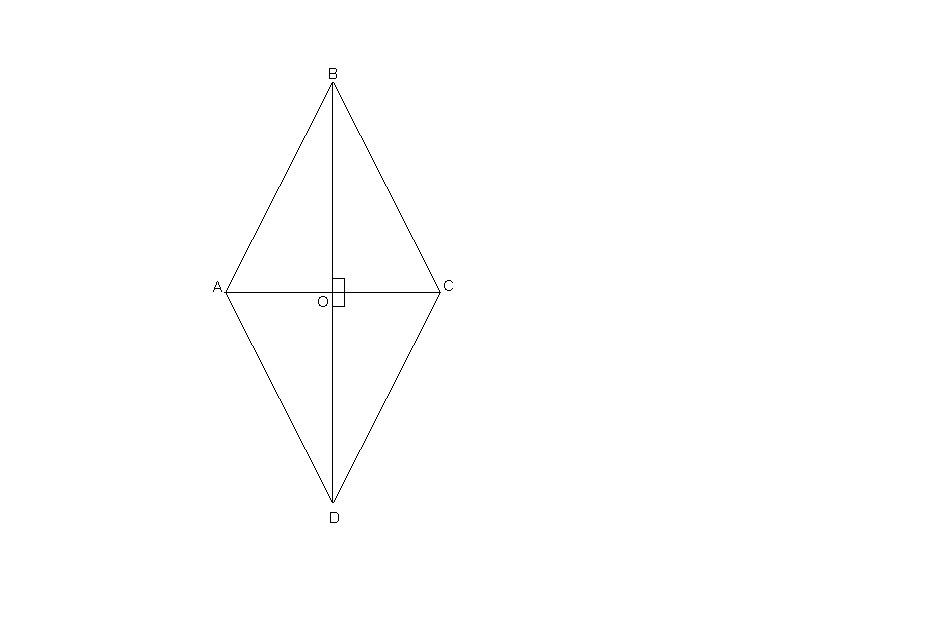
Треугольники ABC и ADC- равносторонние. Отрезки BD и AC пересекаются в точке O. Докажите, что BO=DO AO_|_BD

Пожалуйста очень надо!!!!

Answer 1

Проведем ВО'⊥АС. Так как ΔАВС равносторонний, ВО' - высота и медиана, значит О' - середина АС.
Тогда  в ΔADC DО' - медиана, а следовательно и высота. Т.е. DО'⊥АС.
Через точку О' можно провести единственную прямую, перпендикулярную АС, значит точки В, О' и D лежат на одной прямой, причем точка О' - точка пересечения BD и АС, значит точка О' совпадает с точкой О.
Итак, АО⊥BD.

В равнобедренном ΔABD АО - высота, а значит и медиана. Тогда
BO = OD.