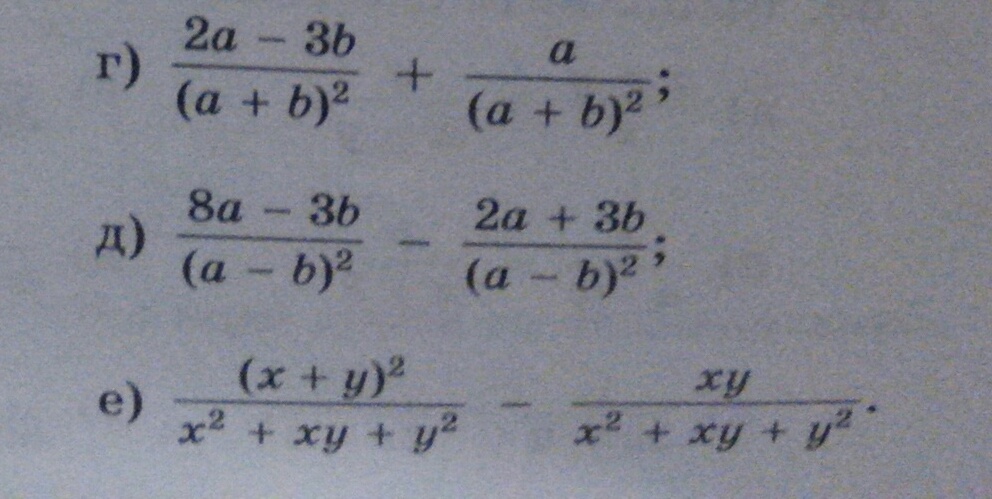Ответы
Ответ дал:
0
дроби с одинаковыми знаменателями, поэтому складываем только числители:

Ответ дал:
0
Ой -3*(a+b)^
Ответ дал:
0
если вынести -3, то в скобке останется (b-a)
Ответ дал:
0
Но с минусом же b
Ответ дал:
0
А все, я поняла
Ответ дал:
0
проверяйте вынесение за скобки мысленным внесением обратно )
Ответ дал:
0
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад