Question

Найти площадь ограниченной фигуры
y=16/x^2, x=4, y=2x
Или хотя бы напишите начальную функцию 16/x^2

Answer 1

Функции $y=dfrac{16}{x^2 }$ отличается от $y=dfrac{16}{x}$ при x>0 тем, что она быстрее убывает. Функция $y=dfrac{16}{x^2 }$ - чётная т.к. степень при единственном "x" чётная.

y=2x - функция прямой пропорциональности (y=kx), её график будет в 3 и 1 четверти (k>0), поэтому пересечении с $y=dfrac{16}{x^2 }$ может быть только в 1 четверти. Такое же и с прямой x=4.

Найдём абсциссу точки пересечения функций $y=dfrac{16}{x^2 }$ и y=2x.

$displaystyle frac{16}{x^2 } =2x;2x^3 =16;x^3 =2^3 \\x=2; frac{16}4 =4=2cdot 2$

Абсцисса точки пересечения графиков функций $y=dfrac{16}{x^2 }$, x=4 и y=2x, x=4 уже известна (x=4).

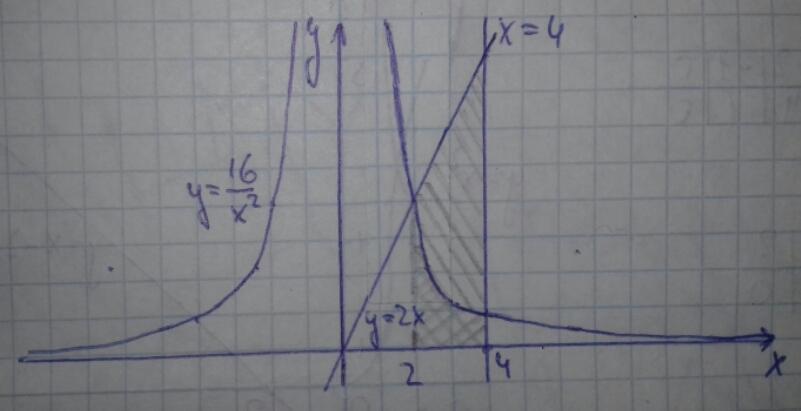
Схематичный график смотри внизу.

Получается, что

$tt displaystyle S=int _2 ^4 2x;dx -int _2 ^4 frac{16}{x^2 } ;dx =int _2 ^4 begin{pmatrix}tt 2x-frac{16}{x^2} end{pmatrix};dx=\\=begin{pmatrix}tt x^2+frac{16}x end{pmatrix} begin{vmatrix}\end{matrix} ^4 _2 =begin{pmatrix}tt 4^2+frac{16}4 end{pmatrix} -begin{pmatrix}tt 2^2+frac{16}2 end{pmatrix} =\\=20-12=8$

Ответ: 8.