Question

ПОМОГИТЕ ЗА 99 БАЛЛОВ
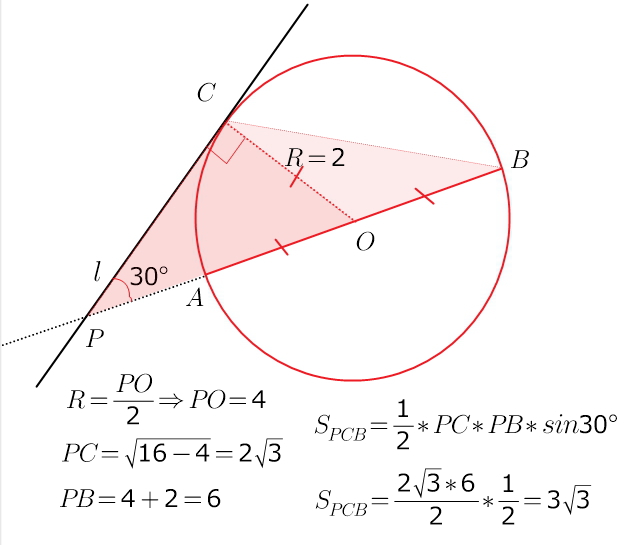
Отрезок АВ - диаметр окружности, центром которой является точка О. Прямая л касается окружности в точке С и пересекает луч АВ в точке Р. Вычислите площадь треугольника РСВ, если длина радиуса окружности равна 2 см и уголСРВ = 30

Answer 1

первое, что нужно вспомнить --- радиус, проведенный в точку касания, перпендикулярен касательной...
получили прямоугольный треугольник РСО с углом в 30°...
про который известно: катет против угла в 30° = половине гипотенузы...
из этого же треугольника по определению косинуса можно записать:
сos30° = √3 / 2 = СР / РО ---> СР = РО*√3 / 2
или то же самое можно получить по т.Пифагора...
а дальше --- известна формула площади треугольника: половина произведения двух сторон на синус угла между ними...
sin30° = 1/2