Question

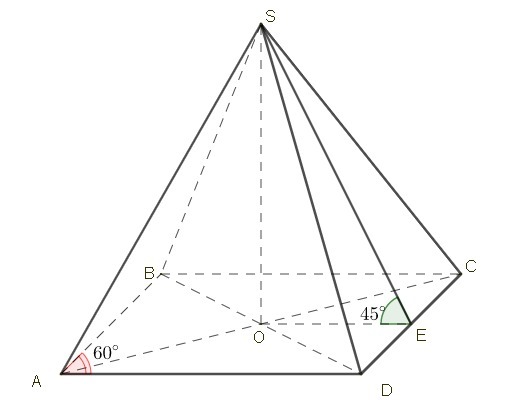
Основание пирамиды-ромб со стороной 14 см и острым углом 60 градусов. Двугранные углы при основании пирамиды равны 45 градусов. Вычислите объём пирамиды.

 

Answer 1

Объем пирамиды вычисляется по формуле $V=dfrac{1}{3}S_{tt o}cdot h$, где $S_{tt o}$ - площадь основания; h - высота пирамиды.

Площадь основания равна $S_{ABCD}=ABcdot ADcdot sin60^circ=98sqrt{3}$ см², с другой стороны она равна $S_{ABCD}=ADcdot h_1$,где $h_1$ - высота ромба ABCD

Приравнивая площади, получим $98sqrt{3}=14h_1$ откуда $h_1=7sqrt{3}$ см

Высота ромба является диаметром вписанной окружности, тогда радиус вписанной окружности равен: $r=OE=dfrac{h_1}{2}=dfrac{7sqrt{3}}{2}$ см

В прямоугольном треугольнике SOE углы OSE и SEO равны, следовательно ΔSOE - равнобедренный прямоугольный треугольник ⇒ $OE=SO=dfrac{7sqrt{3}}{2}$ см

Объём пирамиды: $V=dfrac{1}{3}cdot 98sqrt{3}cdotdfrac{7sqrt{3}}{2}=343$ см³