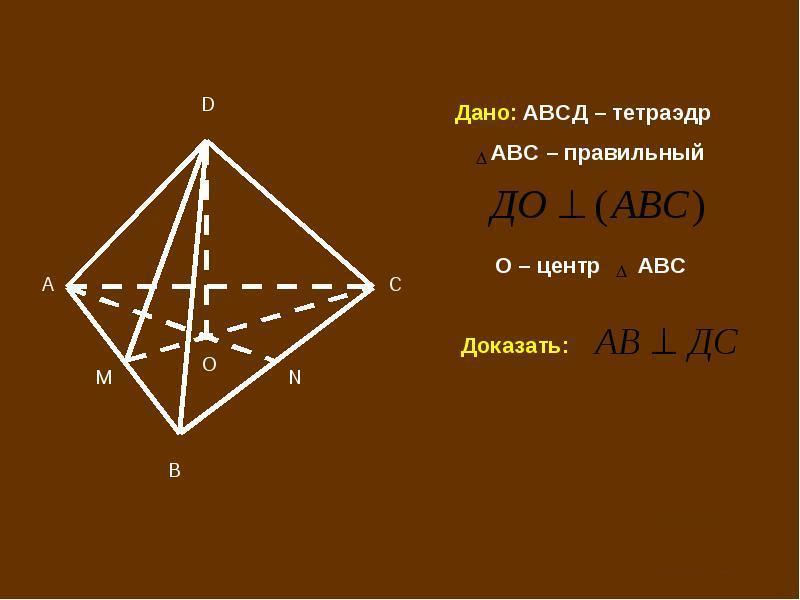
Срочно решить,пожалуйста. 1)В тетраэдре треугольник ABC-правильный. DO перпендикулярно ABC. Доказать, что AB перпендикулярно DC. 2)В тетраэдре ABCD угол DAC = углу DAB. AB=AC.Найти угол между прямыми AD и BC.
Ответы
1) Если О - центр правильного треугольника АВС, то СМ - его высота,
АВ⊥СМ.
DO⊥АВС, значит DO перпендикулярна любой прямой этой плоскости, ⇒
АВ⊥DO.
АВ перпендикулярна двум пересекающимся прямым плоскости DOC, значит перпендикулярна плоскости. Значит прямая АВ перпендикулярна любой прямой, лежащей в плоскости DOC, ⇒
АВ⊥DC.
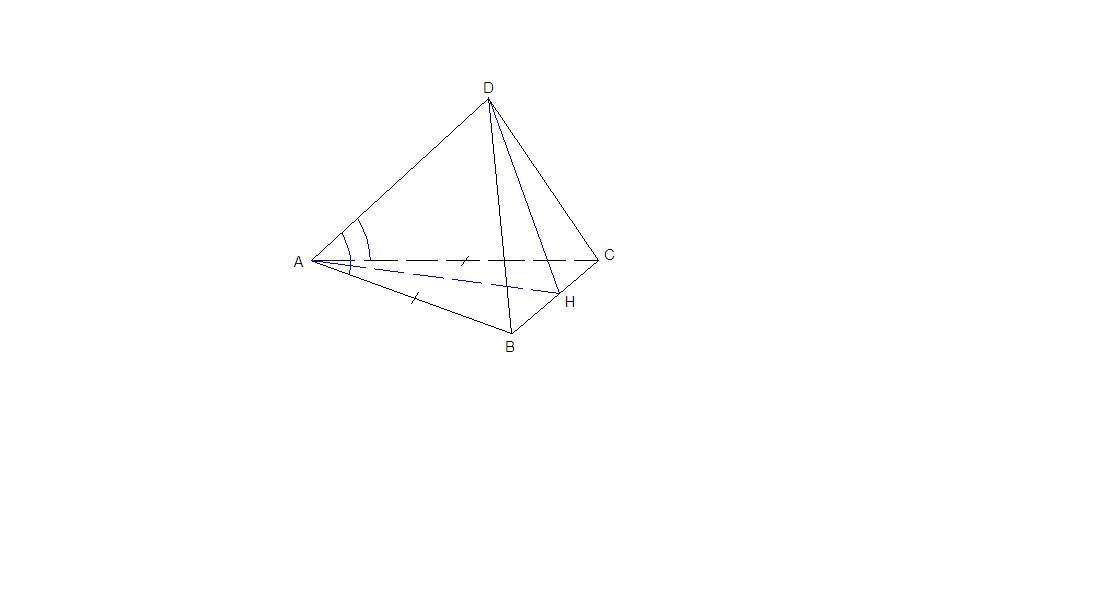
2) АВ = АС по условию, ∠DAC = ∠DAB по условию, DA - общая сторона для треугольников DAC и DAB, значит эти треугольники равны по двум сторонам и углу между ними, ⇒ DC = DB, т.е. ΔDCB равнобедренный.
Пусть Н - середина ВС. Тогда
ВС⊥АН, так как медиана АН равнобедренного треугольника АВС является и высотой,
ВС⊥DH, так как ΔDCB тоже равнобедренный,
ВС перпендикулярна двум пересекающимся прямым плоскости DAH, значит перпендикулярна самой плоскости, значит перпендикулярна каждой прямой этой плоскости, в том числе и AD.
Ответ: угол между прямыми AD и ВС равен 90°.