В квадрате АВСD точка М на стороне АВ и точка N на диагонали АС расположены так, что АМ: МВ = 3: 4, АN: NC = 5: 2. Докажите, что угол DNM прямой.
Ответы
Ответ дал:
0
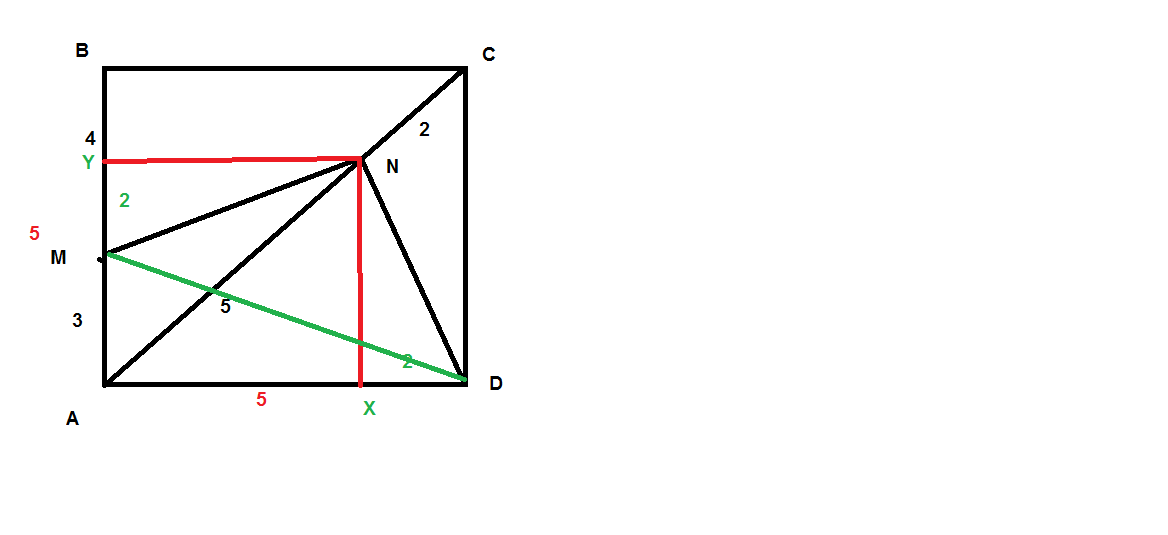
См. рисунок.
т.М делит сторону квадрата в отнош 3:4, соответственно на отрезки 3 и 4 единицы (неважно какие размерности). Сторона квадрата -7 единиц.
т.N делит диагональ в отношении 5:2 ( это уже не 5 и 2 единицы, это только отношение.)
Проведем перпендикуляры (красные линии). Они делят стороны в отношении тоже 5:2, но теперь на 5 и 2 единиц.
И рассмотрим получившиеся треугольники MNY, NDX,MAD

в треугольнике MND

а такое может быть только в прямоугольном треугольнике.
т.М делит сторону квадрата в отнош 3:4, соответственно на отрезки 3 и 4 единицы (неважно какие размерности). Сторона квадрата -7 единиц.
т.N делит диагональ в отношении 5:2 ( это уже не 5 и 2 единицы, это только отношение.)
Проведем перпендикуляры (красные линии). Они делят стороны в отношении тоже 5:2, но теперь на 5 и 2 единиц.
И рассмотрим получившиеся треугольники MNY, NDX,MAD
в треугольнике MND
а такое может быть только в прямоугольном треугольнике.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад