Ответы
Ответ дал:
0
(область) множество значений функции зависит от значений аргумента...
т.е. нужно сначала найти область определения функции D(f)
или ОДЗ...
т.е. нужно сначала найти область определения функции D(f)
или ОДЗ...
Приложения:
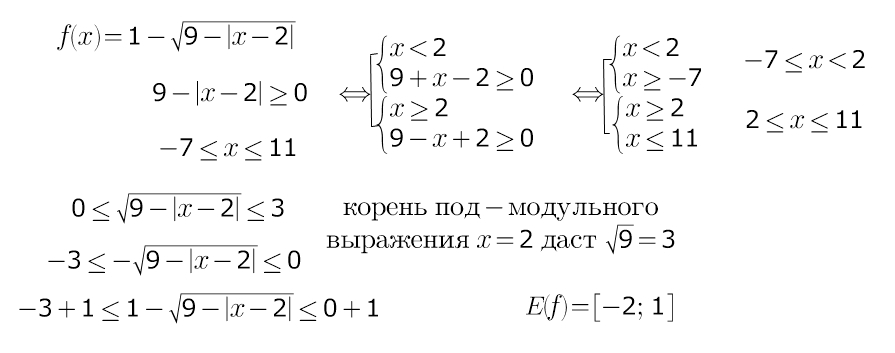

Ответ дал:
0
Внимание !
Ответ дал:
0
спасибо!! исправила))
Ответ дал:
0
f(x) = 1 -√(9 -|x-2|) .
ООФ : 9 -|x-2| ≥0 ⇔ |x-2| ≤ 9 ⇔ -9 ≤ x-2 ≤ 9⇔-7 ≤ x ≤11. x∈[-7;11]
и непрерывно на [-7;11]
f(x) = 1 -√(9 -|x-2|) ≤ 1 т.к. √(9 -|x-2|)≥0
max f(x) =1(меньше отнимаешь, останется больше) ,если 9 -|x-2| =0⇒|x-2| =9; x -2 =± 9 (x₁= -7 ,x₂ =11 (на концах).
----------
min f(x): 1 -3 = -2 .
"больше берут ", меньше останется . max(√(9 -|x-2|) =√9 =3 ,если |x-2| =0, т.е. при x=2 (середине).
ООФ : 9 -|x-2| ≥0 ⇔ |x-2| ≤ 9 ⇔ -9 ≤ x-2 ≤ 9⇔-7 ≤ x ≤11. x∈[-7;11]
и непрерывно на [-7;11]
f(x) = 1 -√(9 -|x-2|) ≤ 1 т.к. √(9 -|x-2|)≥0
max f(x) =1(меньше отнимаешь, останется больше) ,если 9 -|x-2| =0⇒|x-2| =9; x -2 =± 9 (x₁= -7 ,x₂ =11 (на концах).
----------
min f(x): 1 -3 = -2 .
"больше берут ", меньше останется . max(√(9 -|x-2|) =√9 =3 ,если |x-2| =0, т.е. при x=2 (середине).
Приложения:
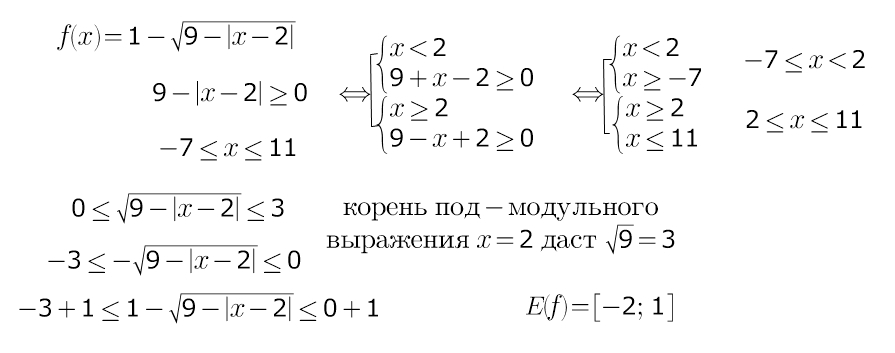

Вас заинтересует
2 года назад
7 лет назад
10 лет назад