Question

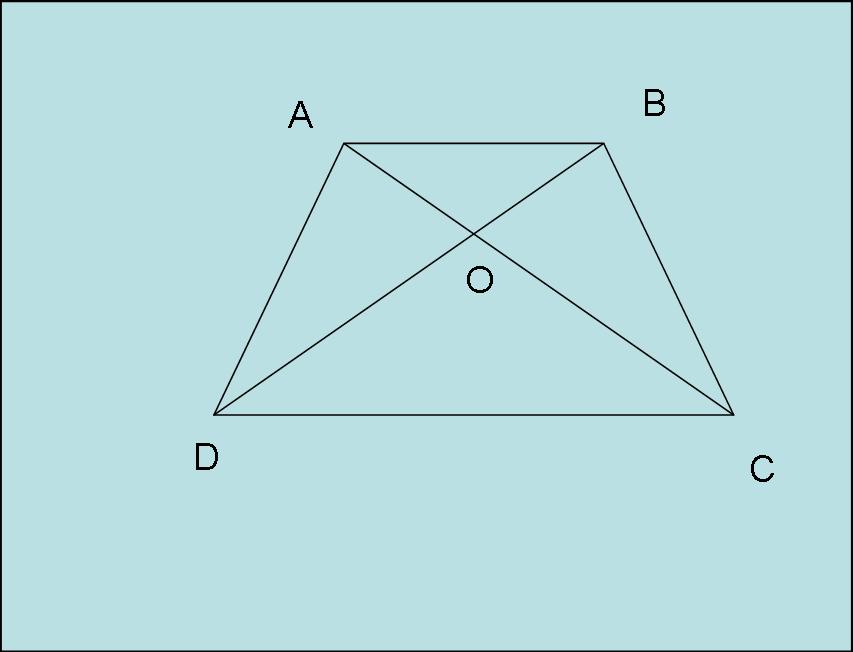
Дана трапеция АВСД Диагонали ВД и АС пересекается в точке О.АВ параллельна СД.а)докажите что АО:ОС=ВО:ОД.б)найдите АВ,если ОД=15 см,ОВ=9 см, СД=25 см

Answer 1

углы AOB и DOC равны как вертикальные

углы BAO и OCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей AC, аналогично равны и углы ABO и ODC.

Следовательно треугольники ABO и CDO подобны по трем углам.

тогда  АО:ОС=ВО:ОД (отношение соответственных сторон) - а)

также AB:DC=OB:DO, следовательно AB=DC*OB/DO=25*9/15=15