Ответы
Ответ дал:
0
Преобразуем выражение:
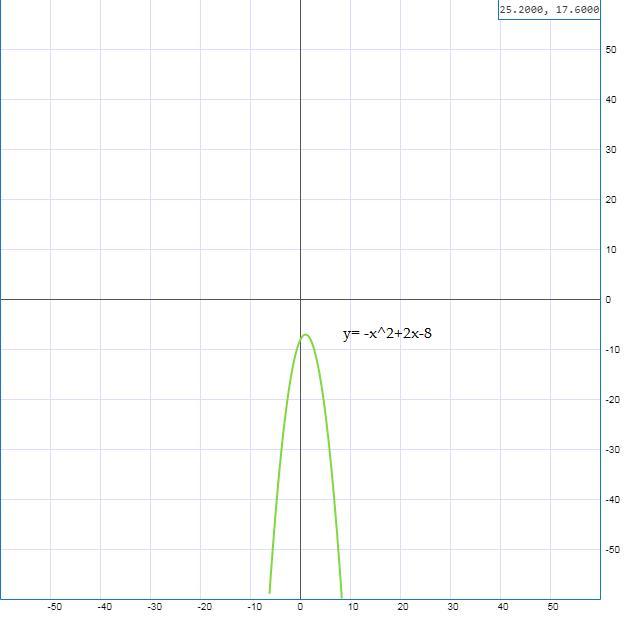
Рассмотрим функцию f(x)= -x²+2x-8
графиком данной функции будет парабола, ветви вниз
Найдем точки пересечения с осью Ох
-x²+2x-8=0\\D=4-4(-1)(-8)=4-32<0
Точек пересечения нет, значит график полностью лежит ниже ось Ох
Таким образом для любых значений а, данное выражение меньше 0
Приложения:
Ответ дал:
0
Видим, что левая часть неравенства всегда отрицательно для всех действительных а.
Приложения:

Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад