Question

Найдите площадь боковой поверхности прямоугольного параллелепипеда, стороны основания коαторого равны a и b а диагональ наклонена к плоскости основания под углом α

Answer 1

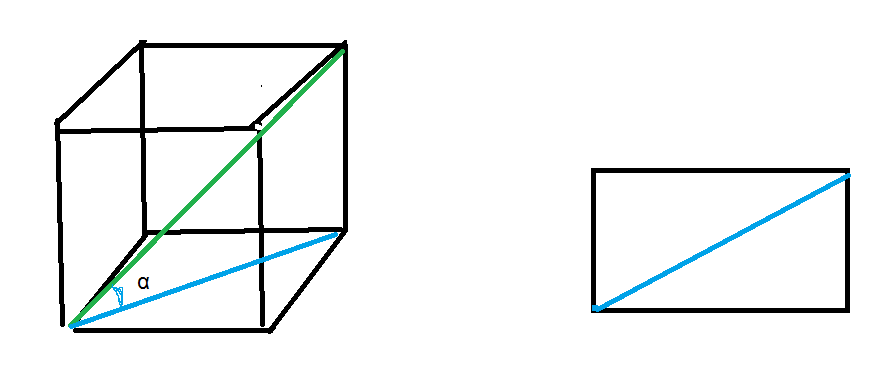
В основании прямоугольник со сторонами а и в. См рисунок в приложении

Диагональ основания  d находим по теореме Пифагора:

$d= sqrt{a^2+b^2}$

Из прямоугольного треугольника с острым углом  α

$H= sqrt{a^2+b^2} cdot tg alpha$

S(бок)=Р(осн)·Н=$=2(a+b)cdot sqrt{a^2+b^2}cdot tg alpha$

Answer 2

Спасибо

Answer 3

только в условии там известна высота,зачем он ее еще раз наешл?

Answer 4

нашел

Answer 5

Там H=3 - высота всей призмы. Для нахождения площади сечения она не нужна

Answer 6

Спасибо Вам большое!