Question

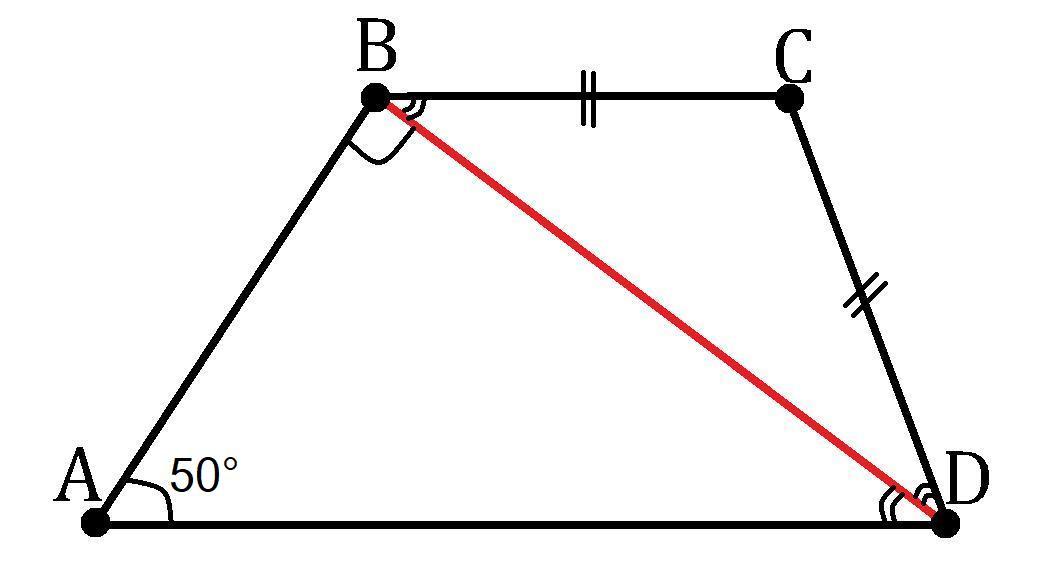
Диагональ трапеции перпендикулярна её боковой стороне, а острый угол, противолежащий этой диагонали, равен 50градусов. Меньшее основание трапеции равно
другой боковой стороне. Найти остальные углы трапеции.

Answer 1

Дано: BC║AD; BD⊥AB; ∠BAD=50°; BC=DC.

Найти: ∠ABC, ∠BCD и ∠CDA.

Решение:

∠BAD+∠ADB+∠DBA = 180° как сумма углов ΔBAD.

∠ADB = 180°-∠DBA-∠BAD = 180°-90°-50° = 40°

∠ADB = ∠DBC как накрест лежащие углы при параллельных прямых BC, AD и секущей DB.

∠DBC = ∠ADB = 40°.

ΔBCD - равнобедренный (по условию BC=DC), поэтому углы при его основании равны (∠DBC=∠BDC).

∠BDC = ∠DBC = 40°.

∠BCD = 180°-∠BDC-∠DBC = 180°-40°-40° = 100° т.к. сумма углов в треугольнике равна 180°.

∠ABC = ∠DBA+∠DBC = 90°+40° =  130°.

∠CDA = ∠ADB+∠BDC = 40°+40° = 80°.

Ответ: 130°, 100° и 80°.