Question

Найдите длину окружности, описанной около правильного треугольника, если радиус вписанной в этот треугольник окружности равен 7 см.

Answer 1

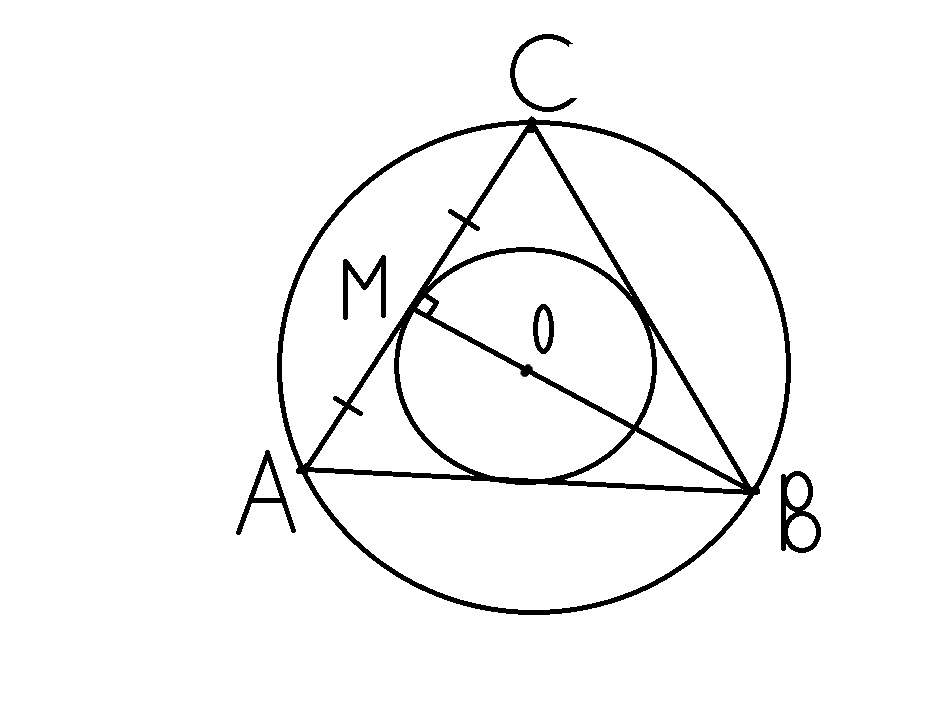
Заметим, что радиус описанной окружности в 2 раза больше радиуса вписанной окружности. Потому что ОМ - радиус вписанной окружности лежит на медиане (которая является биссектрисой и высотой в правильном треугольнике). ВМ - радиус описанной окружности тоже лежит на той же медиане. По свойству медиан - они в точке пересечения дюелятся в отношении 2:1 считая от вершины. Значит ВМ=2*ОМ=2*7=14 см. Длина окружности равна по формуле

$L=2*pi*R=2*pi*14=28piapprox 87.964576$