Question

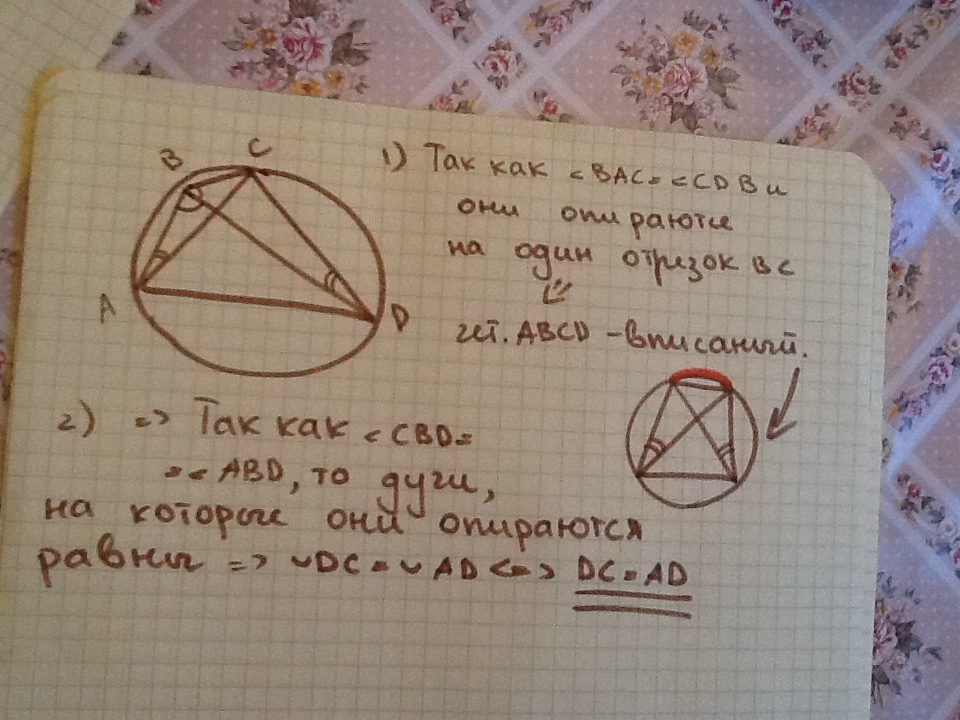
Дан выпуклый четырехугольник ABCD. Известно, что BD - биссектриса в треугольнике ABC и угол BAC=углу BDC. Докажите, что CD=AD.

Answer 1

LFP , вообще не понимаю, где вы в задачке нашли опечатку.... По моему., все нормально;)

Answer 2

Меня сильно смущает утверждение, "если равные углы опираются на один и тот же отрезок, то вершины углов и концы отрезка лежат на одной окружности". Дайте доказательство, пожалуйста.

Answer 3

Прошу меня извинить,доргие господа, но мне казалось, что этот признак вписанного четырехугольника надо знать любому школьнику, собирающемуся знавать ЕГЭ ;) я написала его доказательство на втором листе

Answer 4

Спасибо за доказательство.

Answer 5

нигде в учебнике геометрии ТАК СФОРМУЛИРОВАННОГО "признака вписанного 4-угольника" НЕТ, потому сложно требовать от "любого школьника" знание этого признака... любую задачу по геометрии можно сформулировать как теорему))) выучить это все невозможно, даже собираясь сдавать ЕГЭ... это (на мой взгляд) задача на подобие (здесь легко находятся несколько пар подобных треугольников и доказывается равенство углов (равнобедренность нужного треугольника)))

Answer 6

уже было бы радостно, если бы все, сдающие ЕГЭ, знали о равенстве вписанных углов, опирающихся на одну дугу... а вот об углах, опирающихся на отрезки... это чуть сложнее требовать)))