Question

в каком отношении центр вписанной в треугольник АВС окружности делит биссектрису на AD, если стороны треугольника равны a,b,c?

Answer 1

центр вписанной в треугольник окружности ---это точка пересечения биссектрис треугольника...
обычно сторону против вершины А обозначают (а), против вершины В ---(b)
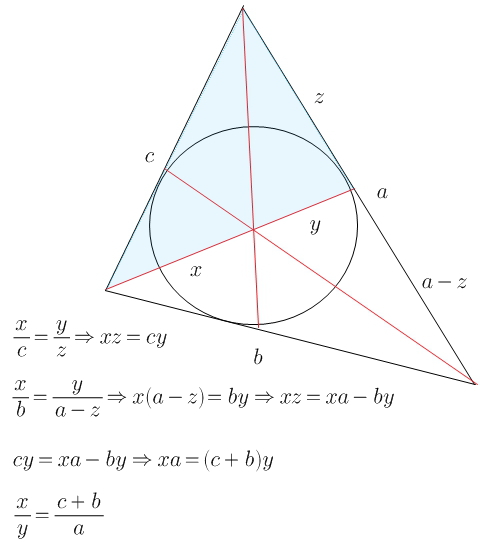
обозначим части биссектрисы AD как (х) и (у)
сторону (а) биссектриса разделит на две части --- обозначим их (z) и (a-z)
искомое отношение х/у
по свойству биссектрис можно записать два отношения (из двух получившихся треугольников:
биссектриса разбивает сторону на два отрезка, пропорциональных прилежащим сторонам)))