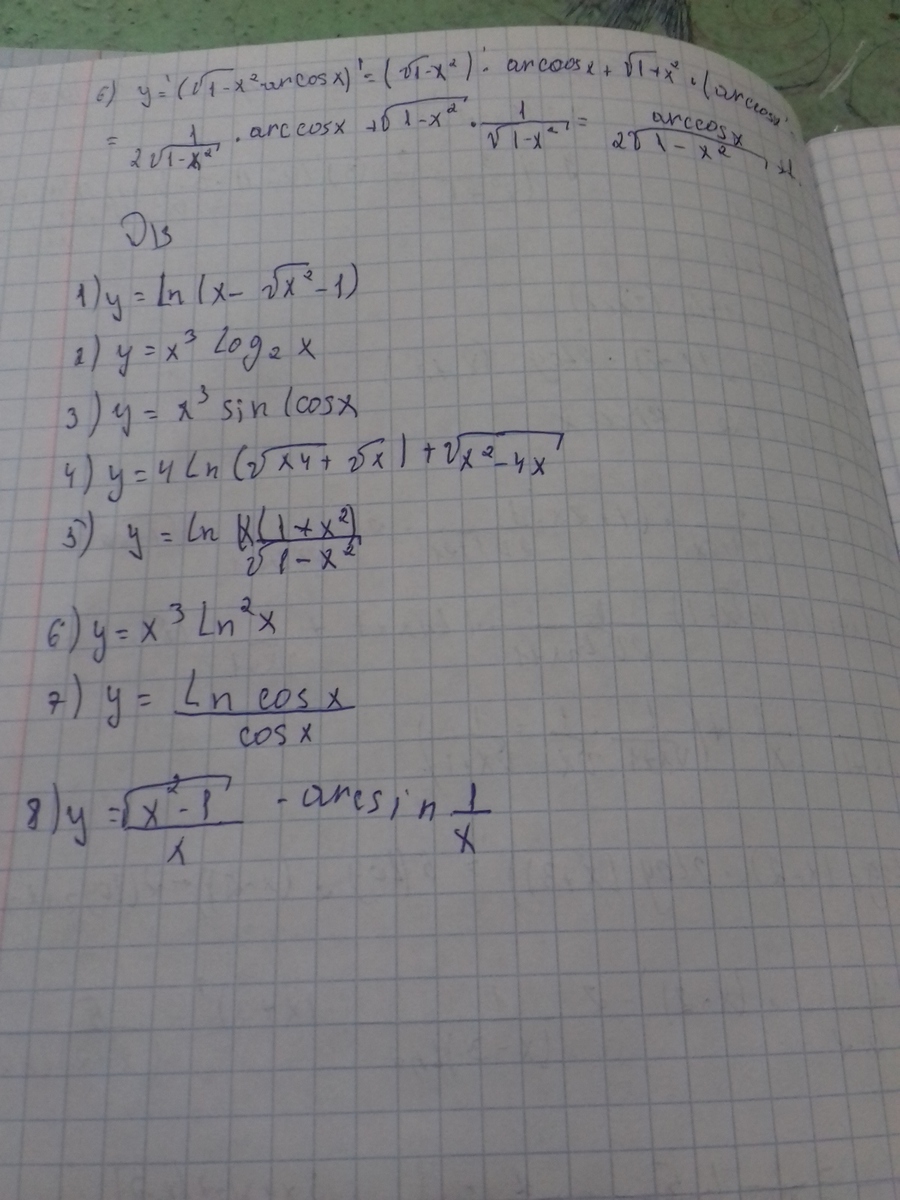Ответы
Ответ дал:
0
1)y=ln(x-√(x²)-1)=ln(x-|x|-1)
при х≥0 у=ln(-1) чего не может быть
при х<0 y=ln(2x-2)
ОДЗ: 2х-2≥0
х≥1/2
y' = 2/(2x-1)
2)y' = х³log₂x=(3x²log₂x)+(x³/(xln2))=x²(3log₂x+(1/ln2))
c третьего по пятое не понятно условие, что стоит между sinx и сosx в третьем, что находится под первым корнем в четвёртом?
6)у' = (3x²ln²x)+(x³2lnx·(1/x))=x²lnx((3lnx)+2)
7)y=(ln(cosx))/(cosx)=(((1/cosx)·(-sinx)·cosx)-ln(cosx)·(-sinx))/cos²x=(-sinx+(ln(cosx)·sinx))/cos²x=(sinx(ln(cosx)-1))/cos²x
в восьмом мне не понятно что за знак стоит между арксинусом и левой частью фунуции
могу решить оставшиеся если уточнишь условие
при х≥0 у=ln(-1) чего не может быть
при х<0 y=ln(2x-2)
ОДЗ: 2х-2≥0
х≥1/2
y' = 2/(2x-1)
2)y' = х³log₂x=(3x²log₂x)+(x³/(xln2))=x²(3log₂x+(1/ln2))
c третьего по пятое не понятно условие, что стоит между sinx и сosx в третьем, что находится под первым корнем в четвёртом?
6)у' = (3x²ln²x)+(x³2lnx·(1/x))=x²lnx((3lnx)+2)
7)y=(ln(cosx))/(cosx)=(((1/cosx)·(-sinx)·cosx)-ln(cosx)·(-sinx))/cos²x=(-sinx+(ln(cosx)·sinx))/cos²x=(sinx(ln(cosx)-1))/cos²x
в восьмом мне не понятно что за знак стоит между арксинусом и левой частью фунуции
могу решить оставшиеся если уточнишь условие
Ответ дал:
0
spasibo
Ответ дал:
0
Я добавила помогите плииз
Ответ дал:
0
а куда добавили?
Ответ дал:
0
посмотрите заданные вопросы мои
Ответ дал:
0
не вижу ничего. можешь сылку в сообщении кинуть?
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад