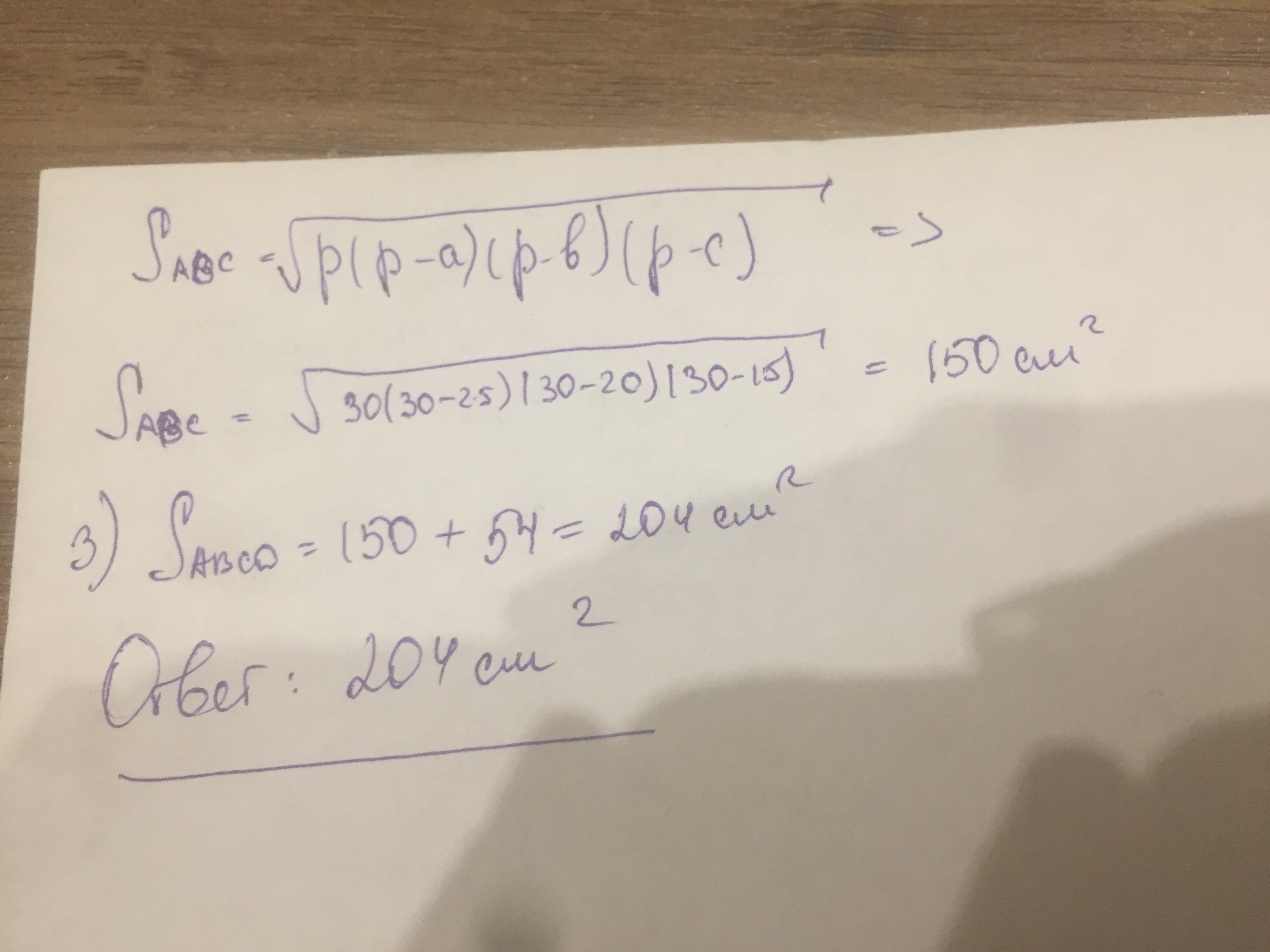Диагональ AC трапеции ABCD делит ее на два подобных треугольника. AB||CD. Найдите площадь трапеции ABCD, если AB = 25cм, BC = 20 см, AC = 15см.
Ответы
Для начала построим треугольник АВС по данным в условии значениям. Заметим, что это пифагоров треугольник, так как АС:ВС:АВ = 3:4:5 (из условия).
Итак, это прямоугольный треугольник с гипотенузой АВ. Проведем через точку С прямую "d" параллельно прямой АВ (дано). Треугольник ADC должен быть прямоугольным, так как сторона АС (диагональ трапеции) делит трапецию на два подобных треугольника (дано). Следовательно, угол АDC=90°.
Рассмотрим треугольники ADC и АВС. Они подобны по условию с коэффициентом подобия k=АC/AB (отношение гипотенуз). Итак k=15/25=3/5.
Тогда из подобия треугольников AD=BC*k = 20*3/5 = 12 см., а
DC = AC*k = 15*3/5 = 9см.
Искомая площадь трапеции АВСD равна S = (AB+CD)*AD/2 = (25+9)*12/2 = 204 см².
Ответ: Sabcd = 204 см².
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!