Формулы сокращённого умножения. Квадрат двучлена.
1. Раскройте скобки:
а)
б)
в)
г)
д)
2. Замените пропуски, отмеченные символом * так, чтобы выполнялось равенство
3. Используя формулы сокращённого умножения для и
, вычислите:
а)
б)
Ответы
Ответ дал:
0
a)t^2+2tm+m^2
б) t^2-6t+9
в) 4t^2+4t+1
г) 9m^2-12mt+4t^2
д) 9m^4+6m^2t^3+t^6
(4a+3b)^2=16a^2+12ab+9b^2
49^2=(50-1)^2=2500-100+1=2401
(20-14/19)^2=
Ответ дал:
0
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Приложения:
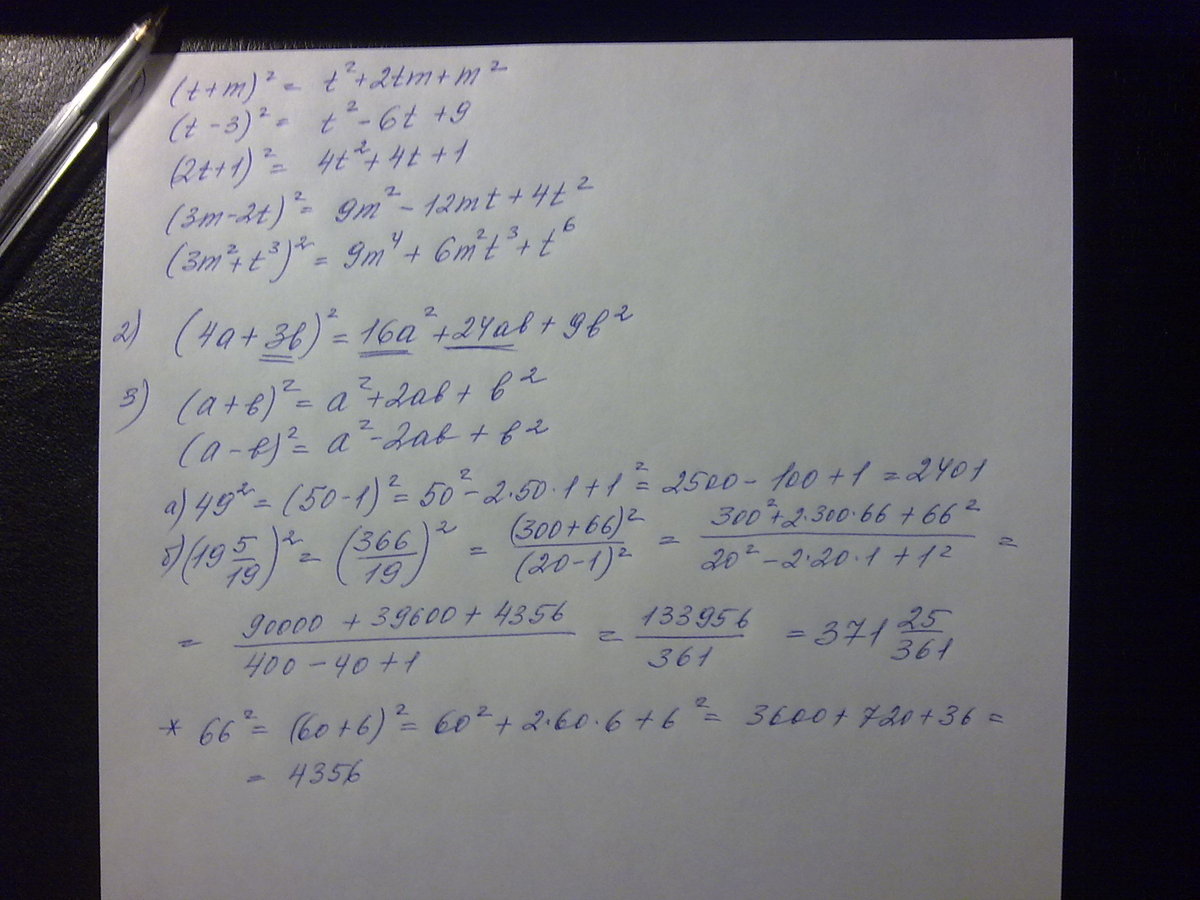

Вас заинтересует
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад