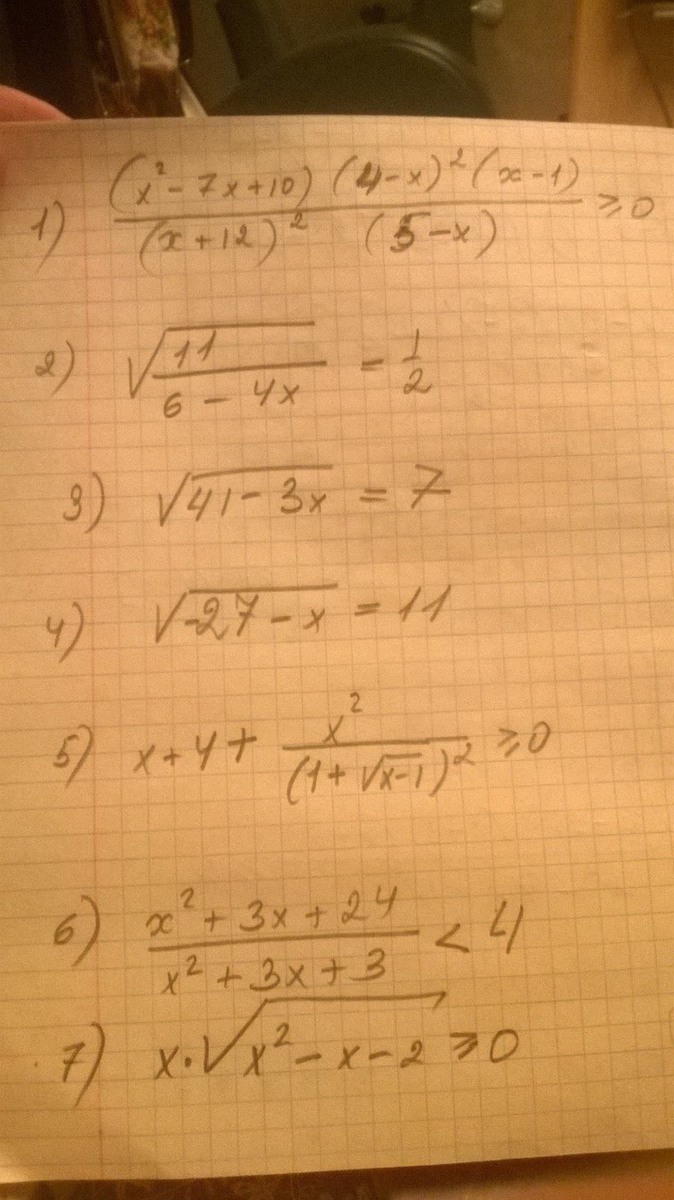Ответы
Ответ дал:
0
1)ОДЗ х≠-12 х≠5
((х-2)(х-5)(4-х)²(х-1))/((x+12)²(5-x))≥0
сократим числитель и знаменатель на (5-х) и внесём оставшийся в числителе минус в скобку (х-2) получится
((2-х)(4-х)²(х-1))/(x+12)²≥0
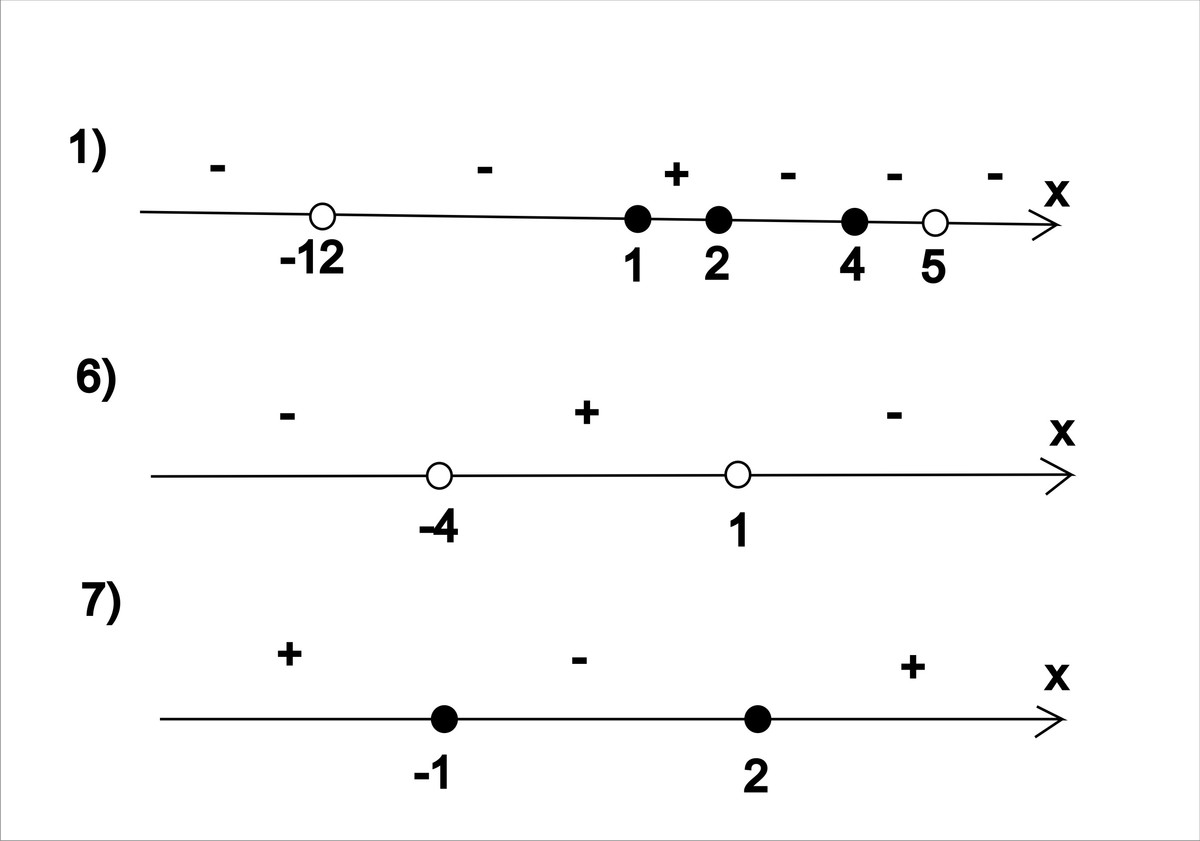
расставим точки как на рисунке затем берём любое значение из каждого интервала и смотрим какой знак будет перед значением дроби
получается х∈[1;2]∨(4)
2)ОДЗ 11/(6-4x)>0 x∈(-∞;3/2)
возводим в квадрат обе части
11/(6-4x)=1/4
44=6-4x
4x=-38
x=-19/2
3)ОДЗ 41-3х>0 x<41/3
возводим в квадрат обе части
41-3x=49
3х=-8
х=-8/3
4)ОДЗ -27-х>0 x<-27
возводим в квадрат обе части
-27-x=121
x=-148
5)ОДЗ х≥1
х²/(1+√(x-1))² всегда будет положительной
х+4 при х≥1 тоже будет положительной
значит х∈[1;+∞)
6)ОДЗ x²+3x+3≠0
рассмотрим уравнение x²+3x+3=0
D=-3<0
Гр-парабола, ветви вверх, значит при всех х x²+3x+3>0
(х²+3х+24-4х²-12х-12)/(x²+3x+3)<0
(-3x²-9x+12)/(x²+3x+3)<0
по скольку знаменатель всегда положительный надо найти
-3х²-9х+12<0
расставим точки как на рисунке, получится
так как выражение у нас должно быть <0 а не ≤0 , то точки -4 и 1 не будут включаться в область решений
х∈(-∞;-4)∨(1;+∞)
7)х·√(х²-х-2)≥0
ОДЗ х²-х-2≥0
х²-2х+х-2≥0
(х+1)(х-2)≥0
х∈(-∞;-1]∨[2;+∞)
на рисунке показана область допустимых значений, а не ответ
получается √(х²-х-2) всегда будет >0
значит при всех х>0 принадлежащих ОДЗ будет выполняться неравенство
значит х∈[2;+∞)
((х-2)(х-5)(4-х)²(х-1))/((x+12)²(5-x))≥0
сократим числитель и знаменатель на (5-х) и внесём оставшийся в числителе минус в скобку (х-2) получится
((2-х)(4-х)²(х-1))/(x+12)²≥0
расставим точки как на рисунке затем берём любое значение из каждого интервала и смотрим какой знак будет перед значением дроби
получается х∈[1;2]∨(4)
2)ОДЗ 11/(6-4x)>0 x∈(-∞;3/2)
возводим в квадрат обе части
11/(6-4x)=1/4
44=6-4x
4x=-38
x=-19/2
3)ОДЗ 41-3х>0 x<41/3
возводим в квадрат обе части
41-3x=49
3х=-8
х=-8/3
4)ОДЗ -27-х>0 x<-27
возводим в квадрат обе части
-27-x=121
x=-148
5)ОДЗ х≥1
х²/(1+√(x-1))² всегда будет положительной
х+4 при х≥1 тоже будет положительной
значит х∈[1;+∞)
6)ОДЗ x²+3x+3≠0
рассмотрим уравнение x²+3x+3=0
D=-3<0
Гр-парабола, ветви вверх, значит при всех х x²+3x+3>0
(х²+3х+24-4х²-12х-12)/(x²+3x+3)<0
(-3x²-9x+12)/(x²+3x+3)<0
по скольку знаменатель всегда положительный надо найти
-3х²-9х+12<0
расставим точки как на рисунке, получится
так как выражение у нас должно быть <0 а не ≤0 , то точки -4 и 1 не будут включаться в область решений
х∈(-∞;-4)∨(1;+∞)
7)х·√(х²-х-2)≥0
ОДЗ х²-х-2≥0
х²-2х+х-2≥0
(х+1)(х-2)≥0
х∈(-∞;-1]∨[2;+∞)
на рисунке показана область допустимых значений, а не ответ
получается √(х²-х-2) всегда будет >0
значит при всех х>0 принадлежащих ОДЗ будет выполняться неравенство
значит х∈[2;+∞)
Приложения:
Ответ дал:
0
Большое спасибо!
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад