Математика вычислить, какие пары плоскостей являются параллельными, а какие - перпендикулярными.
Приложения:
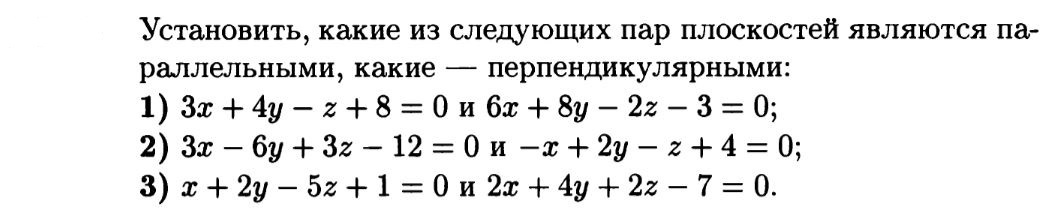
Ответы
Ответ дал:
0
Для плоскости, заданной уравнением

вектор с координатами

является вектором нормали (перпендикулярен к плоскости)
Таким образом, если для двух плоскостей нормальные вектора коллинеарны - то плоскости - параллельны, а если перпендикулярны - то перпендикулярны и плоскости.
Проверим для наших примеров.
a)

Вектора коллинеарны -> плоскости - параллельны
b)

Вектора коллинеарны -> плоскости - параллельны
Более того, для параметра D также верно

т.е. плоскости не просто параллельны, но и совпадают
c)

Вектора не коллинеарны -> плоскости - не параллельны.
Проверим ортогональность векторов

Скалярное произведение векторов равно 0 -> вектора перпендикулярны -> плоскости перпендикулярны
вектор с координатами
является вектором нормали (перпендикулярен к плоскости)
Таким образом, если для двух плоскостей нормальные вектора коллинеарны - то плоскости - параллельны, а если перпендикулярны - то перпендикулярны и плоскости.
Проверим для наших примеров.
a)
Вектора коллинеарны -> плоскости - параллельны
b)
Вектора коллинеарны -> плоскости - параллельны
Более того, для параметра D также верно
т.е. плоскости не просто параллельны, но и совпадают
c)
Вектора не коллинеарны -> плоскости - не параллельны.
Проверим ортогональность векторов
Скалярное произведение векторов равно 0 -> вектора перпендикулярны -> плоскости перпендикулярны
Ответ дал:
0
А как мы получили коэффициент 1/2 под буквой а)
Ответ дал:
0
Так визуально видно... поделите первые координаты друг на друга... для первой плоскости A=3 для второй A=6... вот и коэффициент...
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад