Диагонали прямоугольника ABCD пересекаются в точке M,AB=7,AC=12.Найдите периметр треугольника ABM.
Ответы
Ответ дал:
0
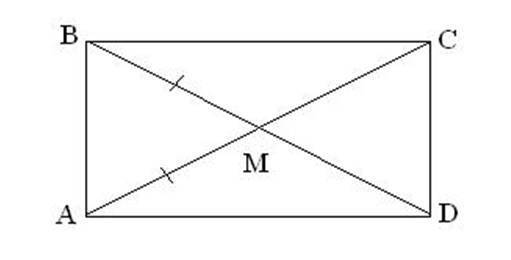
См. рис. к задаче в приложении.
Пусть дан прямоугольник АВСD, диагонали которого пересекаются в точке М. АВ = 7 см, АС = 12 см. Найдем периметр ΔАВМ.
Диагонали прямоугольника равны , а т.к. прямоугольник - это также и параллелограмм, то диагонали точкой пересечения делятся пополам, т.е. АМ = МС = ВМ = МD = АС : 2 = 12 : 2 = 6 (см). Тогда периметр ΔАВМ равен:
Р(ΔАВМ) = АВ + АМ + ВМ = 7 + 6 + 6 = 19 (см)
Ответ: 19 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад