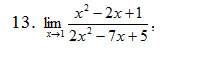Ответы
Ответ дал:
0
Разложим числитель и знаменатель на множители
x²-2x+1=0
D=4-4=0
x=1
x²-2x+1=(x-1)(x-1)=(x-1)²
2x²-7x+5=0
D=49-40=9
x₁=
x₂=
2x²-7x+5=
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад