Ответы
Ответ дал:
0
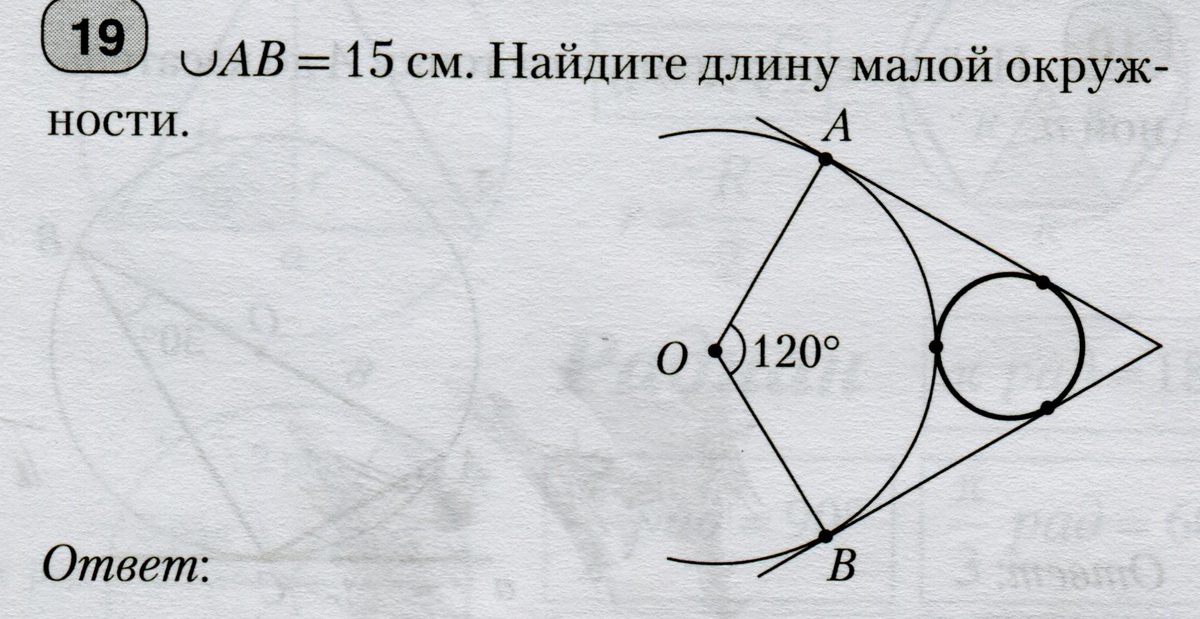
Обозначим точку пересечения касательных за С. центр меньшей окружности за О1..
Угол АСО = 90 - (120/2) = 90 - 60 = 30°.
Находим радиус дуги в 120°:
Отрезок ОС, лежащий против угла в 30°, равен 2R.
Отрезок О1С = 2r.
Составим уравнение: ОС = R + r + 2r = R + 3r.
Заменим ОС = 2R.
Тогда 2R = R + 3r.
Или R = 3r.
Отсюда .
.
Длина малой окружности равна:
 см.
см.
Угол АСО = 90 - (120/2) = 90 - 60 = 30°.
Находим радиус дуги в 120°:
Отрезок ОС, лежащий против угла в 30°, равен 2R.
Отрезок О1С = 2r.
Составим уравнение: ОС = R + r + 2r = R + 3r.
Заменим ОС = 2R.
Тогда 2R = R + 3r.
Или R = 3r.
Отсюда
Длина малой окружности равна:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад