Ответы
Ответ дал:
0
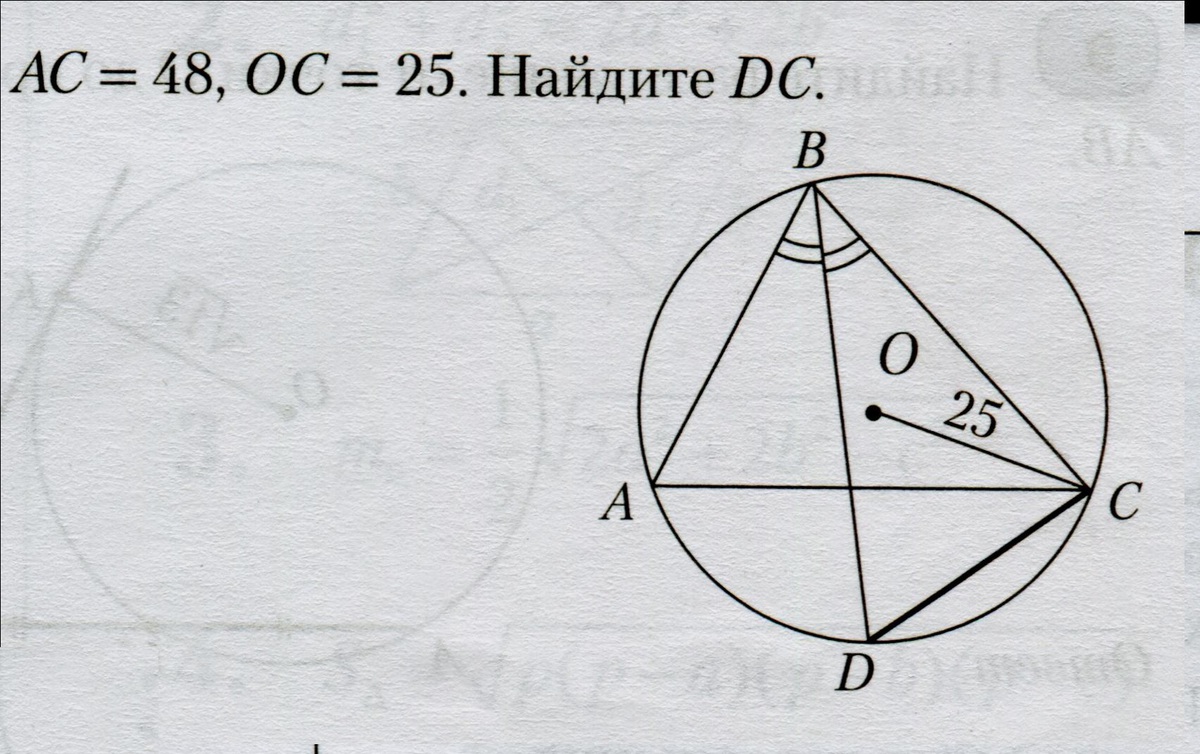
Вписанные углы АВD и СВD равны по условию, следовательно, опираются на равные дуги АD и СD.
Хорды, стягивающие равные дуги окружности. равны.
Треугольник АDС - равнобедренный.
ОD = перпендикулярно АС по свойству радиуса и высоты равнобедренного треугольника.
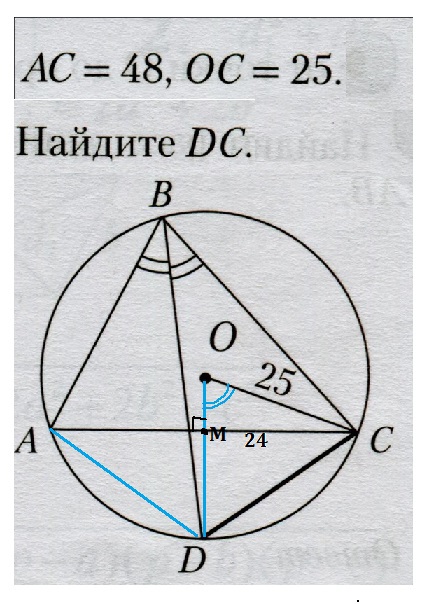
В прямоугольном треугольнике ОСМ катет ОМ=7 ( треугольник из .Пифагоровых троек, можно проверить по т. Пифагора)
ОD=ОС=25 - радиус.
МD=25-7=18
В прямоугольном треугольнике гипотенуза
DС=√(МС²+МD²)=√900=30
DС=30
Хорды, стягивающие равные дуги окружности. равны.
Треугольник АDС - равнобедренный.
ОD = перпендикулярно АС по свойству радиуса и высоты равнобедренного треугольника.
В прямоугольном треугольнике ОСМ катет ОМ=7 ( треугольник из .Пифагоровых троек, можно проверить по т. Пифагора)
ОD=ОС=25 - радиус.
МD=25-7=18
В прямоугольном треугольнике гипотенуза
DС=√(МС²+МD²)=√900=30
DС=30
Приложения:
Ответ дал:
0
спасибо, а подскажите пожалуйста, без пифагоровых троек здесь нельзя?
Ответ дал:
0
Обязательно можно. Пифагоровых троек много, знание хотя бы некоторых из них помогает при решении. задач. В записи решения написано, что можно проверить по т. Пифагора значение ОМ. В прямоугольном треугольнике ОСМ гипотенуза=25, катет=24. По т.Пифагора квадрат гипотенузы равен сумме квадратов катетов. 625=576-ОМ². Отсюда второй катет ОМ=√49=7
Ответ дал:
0
Спасибо, что ответили! Да, я поняла, что проверив все сойдется, ! Я имела ввиду, если без знания того, что это треугольник из Пифагоровых троек и что катет равен 7, можно ли найти другим способом...
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад