Question

ОЧЕНЬ СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА!!! В основании пирамиды лежит равнобедренный треугольник с основанием 12 см. Боковые грани пирамиды,содержащие боковые стороны треугольника,перпендикулярны
плоскости основания,а третья грань образует с основанием угол 30 градусов. Найти площадь полной поверхности пирамиды,если ее высота равна = 8 корней из 3 см.!!!!!!

Answer 1

две боковые грани пирамиды равны (по двум катетам)))
катет против угла в 30° равен половине гипотенузы)))
площадь полной поверхности = сумма площадей боковых граней)))

Answer 2

Огромное спасибо LTP.
-------------------------------
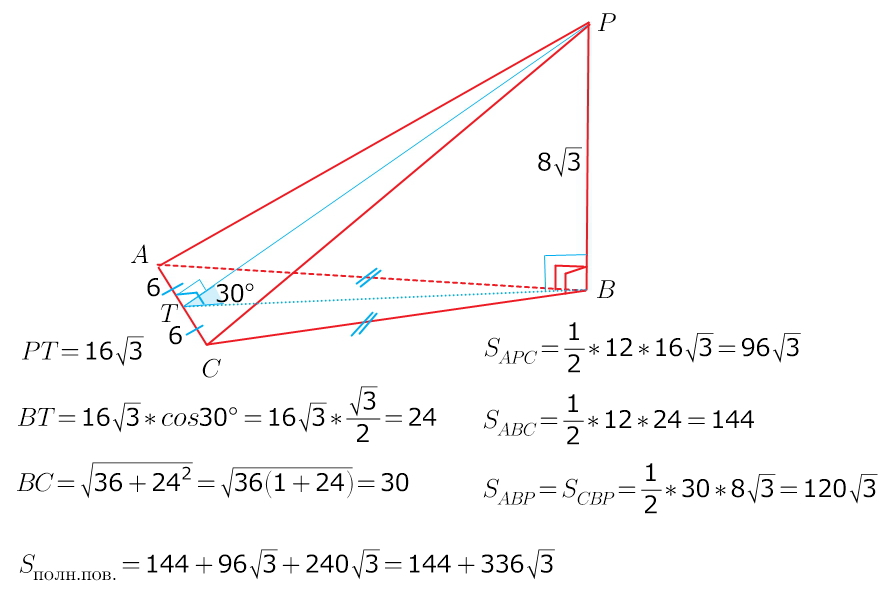
Пусть  ΔABC  основание пирамиды : AB =BC  , AC =12 и BT его медиана . 
(APB)⊥ (ABC)  и  (CPB)⊥ (ABC)  ⇒ PB ⊥(ABC) , следовательно PB⊥ BT.
---------
BT⊥ AC ( медиана BT в ΔABC  одновременно является  и высотой). 
Из  ΔAPB= ΔCPB  ⇒PA=PC, поэтому   PT ⊥ AC ( медиана  PT в ΔAPC   одновременно является  и высотой) . Таким образом ∠PTB  является линейным углом двугранного угла   PACB и по условию задачи∠PTB =30°.