Question

Пожалуйста, помогите решить

Answer 1

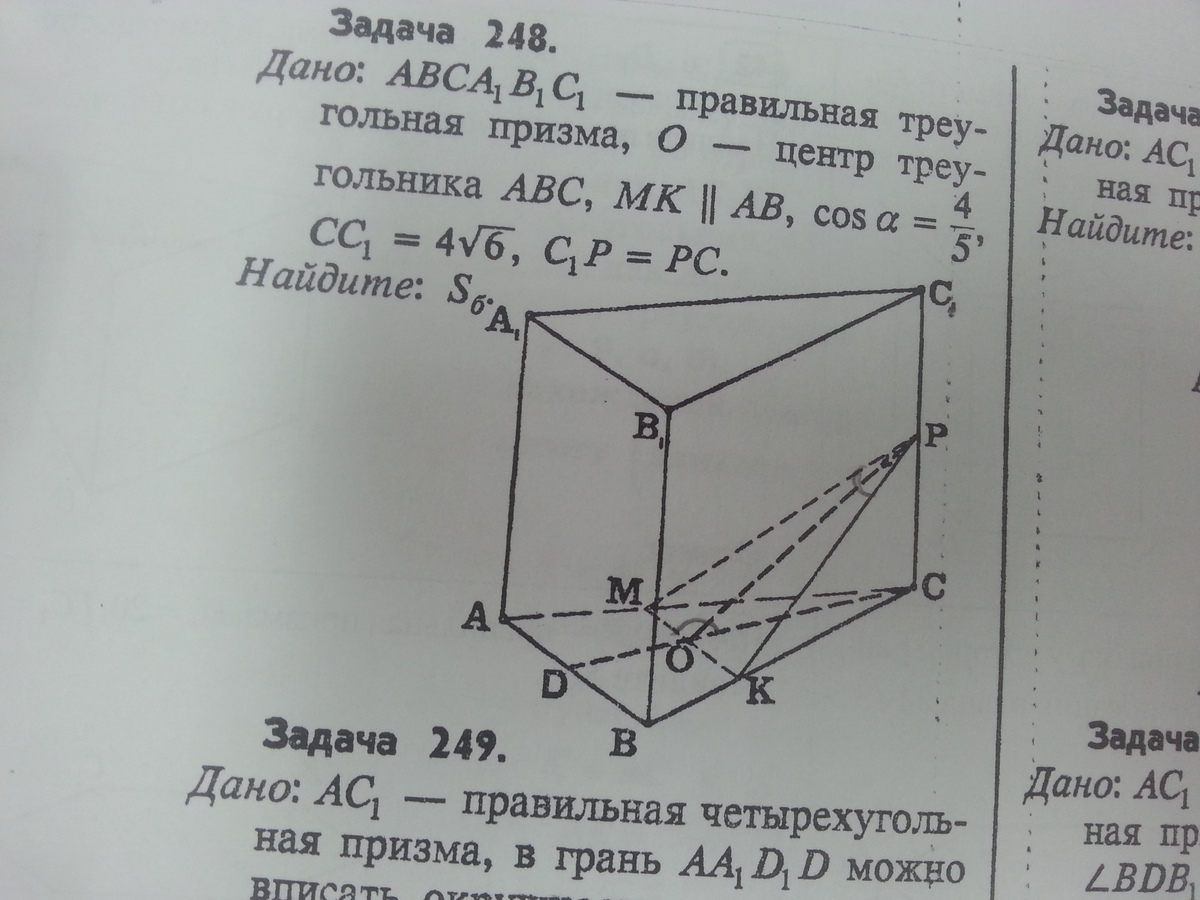
№248) Обозначим сторону основания за х.
Так как центр делит высоту СД в отношении 2/3 от вершины, то МК = (2/3)х. Треугольник АВС - правильный, то и подобный ему СМК - тоже правильный. СК = МК = (2/3)х.
Отрезок РК на боковой грани равен по Пифагору:
$PK= sqrt{CK^2+PC^2} = sqrt{ frac{4x^2}{9}+( frac{4 sqrt{6} }{2})^2 } = frac{2}{3} sqrt{x^2+54}$.
Из треугольника МРК имеем РК = ОК / sin (α / 2).
$PK= frac{x}{3sin frac{ alpha }{2} }$.
Составим уравнение:
$frac{x}{3sin frac{ alpha }{2} } = frac{2}{3} sqrt{x^2+54}$.
Используем формулу преобразования:
$sin frac{ alpha }{2}=+- sqrt{ frac{1-cosx}{2} }= sqrt{ frac{1- frac{4}{5} }{2} } = frac{1}{ sqrt{10} }$.
Найдём $cos frac{ alpha }{2}= sqrt{1-sin^2 frac{ alpha }{2} } = sqrt{1- frac{1}{10} } = frac{3}{ sqrt{10} }$.
Подставим полученное значение sin(α/2) в уравнение, сократим на 3 и возведём обе части в квадрат:
10х² = 4х² + 216
6х² = 216
х² = 36
х = 6 - это сторона основания.
МК = (2/3)х = (2/3)*6 = 4.
РК = 6 /(3*(1/√10)) = 2√10
Высота ОР = РК*cos(α/2) = 2√10*(3/√10) = 6.
Тогда площадь треугольника МРК равна:
 S(МРК) = (1/2)4*6 = 12 кв.ед.

Answer 2

Спасибо)