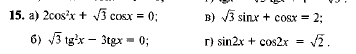Ответы
Ответ дал:
0
а) решаем как неполное квадратное:
Cos x(2Cos x + √3) = 0
Cos x = 0 или 2Сos x + √3 = 0
x = π/2 + πk , k ∈Z 2Cos x = -√3
Cos x = -√3/2
x = +-arcCos(-√3/2) + 2πn , n ∈Z
x = +- 5π/6 + 2πn , n ∈Z
б) Решаем как неполное квадратное:
tg x(√3 tgx -3) = 0
tg x = 0 или √3 tgx -3 = 0
x = πn, n ∈Z √3 tg x = 3
tg x = 3/√3 = √3
x = π/3 + πk , k ∈Z
в) √3 Sin x + Cos x = 0 |:2
√3/2 Sin x + 1/2Cos x = 0
Sin π/3 Sin x + Cos π/3 Cos x = 0
Cos(π/3 -x) = 0
π/3 - х = π/2 + πk , k ∈ Z
-x = -π/3 + π/2 + πk, k ∈Z
-х = π/6 + πk , k ∈Z
x = -π/6 - πk, k ∈Z
г) Sin 2x + Cos 2x = √2 | : √2
1/√2 ·Sin 2x + 1/√2·Cos 2x =1
Sinπ/4 Sin 2x + Cos π/4 Cos 2x = 1
Cos(π/4 - 2x) = 1
π/4 - 2x = 2πk , k ∈Z
-2x = -π/4 + 2πk , k ∈Z
х = π/8 - πk , k ∈Z
Cos x(2Cos x + √3) = 0
Cos x = 0 или 2Сos x + √3 = 0
x = π/2 + πk , k ∈Z 2Cos x = -√3
Cos x = -√3/2
x = +-arcCos(-√3/2) + 2πn , n ∈Z
x = +- 5π/6 + 2πn , n ∈Z
б) Решаем как неполное квадратное:
tg x(√3 tgx -3) = 0
tg x = 0 или √3 tgx -3 = 0
x = πn, n ∈Z √3 tg x = 3
tg x = 3/√3 = √3
x = π/3 + πk , k ∈Z
в) √3 Sin x + Cos x = 0 |:2
√3/2 Sin x + 1/2Cos x = 0
Sin π/3 Sin x + Cos π/3 Cos x = 0
Cos(π/3 -x) = 0
π/3 - х = π/2 + πk , k ∈ Z
-x = -π/3 + π/2 + πk, k ∈Z
-х = π/6 + πk , k ∈Z
x = -π/6 - πk, k ∈Z
г) Sin 2x + Cos 2x = √2 | : √2
1/√2 ·Sin 2x + 1/√2·Cos 2x =1
Sinπ/4 Sin 2x + Cos π/4 Cos 2x = 1
Cos(π/4 - 2x) = 1
π/4 - 2x = 2πk , k ∈Z
-2x = -π/4 + 2πk , k ∈Z
х = π/8 - πk , k ∈Z
Ответ дал:
0
спасибо большое!
Ответ дал:
0
Рад, если помог.
Ответ дал:
0
пример в) √3sinx +cosx = 2 , а не √3sinx +cosx = 0
Ответ дал:
0
15.
a) 2cos²x +√3cosx=0 ;
2cosx(cosx +(√3)/2 )=0 ;
[ cosx =0 ;cosx +(√3)/2=0 .⇒[x =π/2+πn ; x = ±(π-π/6) +2πn , n∈Z.
ответ :π/2+πn , ±5π/6) +2πn , n∈Z.
------
б)√3tq²x -3tqx=0 ;
√3tqx(tqx -√3) = 0 ;
[ tq =0 ; tq= -√3. ⇒ [ x = πn ; x = -π/3+ πn , n∈Z.
ответ :πn , -π/3) +πn , n∈Z.
------
в)√3sinx +cosx = 2 ; * * * метод вспомогательного угла * * *
(√3)/2 *sinx +(1/2)* cosx =1 ;
sinxcosπ/6 + cosxsinπ/6 =1 ;
sin(x+π/6 )=1 ;
x+π/6 =π/2+2πn ,n∈Z.
x = π/3 + 2πn ,n∈Z.
ответ :πn , -π/3) +πn , n∈Z.
------
г) sin2x +cos2x =√2 ;
√2sin(2x+π/4) =√2 ;
sin(2x+π/4) =1 ;
2x+π/4 =π/2+2πn ,n∈Z.
x =π/8+ πn , n∈Z.
ответ :π/8 +πn , n∈Z.
------
удачи !
a) 2cos²x +√3cosx=0 ;
2cosx(cosx +(√3)/2 )=0 ;
[ cosx =0 ;cosx +(√3)/2=0 .⇒[x =π/2+πn ; x = ±(π-π/6) +2πn , n∈Z.
ответ :π/2+πn , ±5π/6) +2πn , n∈Z.
------
б)√3tq²x -3tqx=0 ;
√3tqx(tqx -√3) = 0 ;
[ tq =0 ; tq= -√3. ⇒ [ x = πn ; x = -π/3+ πn , n∈Z.
ответ :πn , -π/3) +πn , n∈Z.
------
в)√3sinx +cosx = 2 ; * * * метод вспомогательного угла * * *
(√3)/2 *sinx +(1/2)* cosx =1 ;
sinxcosπ/6 + cosxsinπ/6 =1 ;
sin(x+π/6 )=1 ;
x+π/6 =π/2+2πn ,n∈Z.
x = π/3 + 2πn ,n∈Z.
ответ :πn , -π/3) +πn , n∈Z.
------
г) sin2x +cos2x =√2 ;
√2sin(2x+π/4) =√2 ;
sin(2x+π/4) =1 ;
2x+π/4 =π/2+2πn ,n∈Z.
x =π/8+ πn , n∈Z.
ответ :π/8 +πn , n∈Z.
------
удачи !
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад