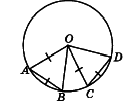
На рисунке точка O-центр окружности, AO=AB, OC=CD. Докажите, что треугольник AOB=COD
Приложения:
Ответы
Ответ дал:
0
в тр-ке АОВ ОA=ОВ=r
значит, тр-ник АОВ – равносторонний, тогда угол О = 60°
в тр-ке СОD ОC=ОD=r
значит, тр-ник CОD – равносторонний, тогда угол О = 60°
Δ AOB= Δ COD ( по 2 стор. и углу м/у ними), т.к.
1) ОА=ОС (как радиусы)
2) ОВ=ОD (как радиусы)
3) ∠AOB = ∠ COD = 60° Чтд.
значит, тр-ник АОВ – равносторонний, тогда угол О = 60°
в тр-ке СОD ОC=ОD=r
значит, тр-ник CОD – равносторонний, тогда угол О = 60°
Δ AOB= Δ COD ( по 2 стор. и углу м/у ними), т.к.
1) ОА=ОС (как радиусы)
2) ОВ=ОD (как радиусы)
3) ∠AOB = ∠ COD = 60° Чтд.
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад