Помогите решить эти задачи, пожалуйста)
1. Найдите все углы, образовавшиеся при пересечении двух параллельных прямых а и b секущей c, если один из углов в 5 раз больше другого.
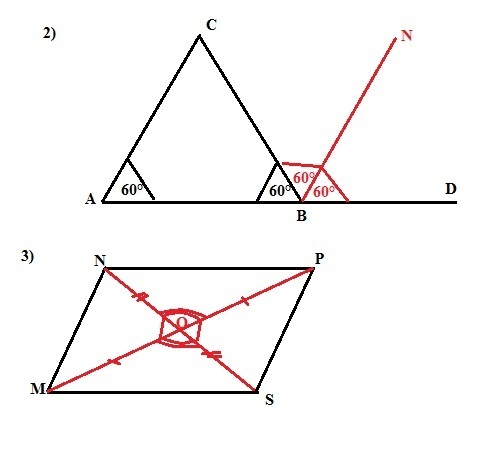
2. В равнобедренном треугольнике АВС с основанием АВ, угол А равен 60 градусов. Докажите, что биссектриса ВN угла СВД (Д лежит на прямой АВ), смежного с углом В треугольника, параллельна АВ.
3. Дан четырёхугольник MNPS. Отрезки MP и NS пересекаются в точке О , так что MO =OP, NO = OS. Докажите, что MS || NP MN || PS.
Ответы
Ответ дал:
0
1. При пересечении двух параллельных прямых третьей
образуется 8 углов - по 4 в каждой точке пересечения: 1 - 4 и 5 - 8 смежные и вертикальные. Группы из 4 углов связаны между собой углами 3 и 6, 4 и 5 - накрест лежащие и 3 и 5, 4 и 6 - односторонние.
вертикальные и накрест лежащие равны между собой, а смежные и односторонние в сумме равны 180°.
Так как нам даны разные углы, то это углы смежные или односторонние. Таким образом, можем записать, что градусные меры этих углов относятся как 1:5, то есть в сумме равны 1х+5х=6х =180°. Отсюда х=30°.Пусть <2=x=30°. Тогда <1= 150°.
Ответ: <1,<4,<5,<8 =150°, а <2,<3,<6,<7 = 30°
2. В условии явная ошибка. Должно быть: "Докажите, что биссектриса ВN угла СВД (Д лежит на прямой АВ), смежного с углом В треугольника, параллельна АС" , так как точки А,В, и D лежат на одной прямой, а биссектриса BN пересекает эту прямую.
Решение.
Угол А при основании АВ равен 60°, следовательно и <B =60°. Смежный с этим углом <CBD = 180°-60°=120°, а биссектриса BN делит его пополам. Следовательно, <NBD=60° и он равен <A, а это соответственные углы при прямых АС и BN и секущей АD. Значит
прямые АС и BN параллельны, что и требовалось доказать.
3. Треугольники MOS и NOP, MON и POS попарно равны по двум сторонам и углу между ними (равенство сторон дано, а углы - вертикальные).
Из равенства треугольников следует равенство сторон MS и NP,
MN и PS. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник - параллелограмм и MS||MP, а MN||PS, что и требовалось доказать.
образуется 8 углов - по 4 в каждой точке пересечения: 1 - 4 и 5 - 8 смежные и вертикальные. Группы из 4 углов связаны между собой углами 3 и 6, 4 и 5 - накрест лежащие и 3 и 5, 4 и 6 - односторонние.
вертикальные и накрест лежащие равны между собой, а смежные и односторонние в сумме равны 180°.
Так как нам даны разные углы, то это углы смежные или односторонние. Таким образом, можем записать, что градусные меры этих углов относятся как 1:5, то есть в сумме равны 1х+5х=6х =180°. Отсюда х=30°.Пусть <2=x=30°. Тогда <1= 150°.
Ответ: <1,<4,<5,<8 =150°, а <2,<3,<6,<7 = 30°
2. В условии явная ошибка. Должно быть: "Докажите, что биссектриса ВN угла СВД (Д лежит на прямой АВ), смежного с углом В треугольника, параллельна АС" , так как точки А,В, и D лежат на одной прямой, а биссектриса BN пересекает эту прямую.
Решение.
Угол А при основании АВ равен 60°, следовательно и <B =60°. Смежный с этим углом <CBD = 180°-60°=120°, а биссектриса BN делит его пополам. Следовательно, <NBD=60° и он равен <A, а это соответственные углы при прямых АС и BN и секущей АD. Значит
прямые АС и BN параллельны, что и требовалось доказать.
3. Треугольники MOS и NOP, MON и POS попарно равны по двум сторонам и углу между ними (равенство сторон дано, а углы - вертикальные).
Из равенства треугольников следует равенство сторон MS и NP,
MN и PS. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник - параллелограмм и MS||MP, а MN||PS, что и требовалось доказать.
Приложения:

Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад