Диагонали ромба ABCD пересекаются в точке O, и диагональ BD равна стороне ромба. Найдите угол между векторами: а) AB и AD; б) AB и DA; в) BA и AD; г) OC и OD; д) AB и CD
Желательно объяснить КАК РЕШИТЬ хотя бы одно
Ответы
Ответ дал:
0
Пусть стороны ромба  .
.
Тогда и диагональ . Так как диагонали ромба делятся точкой пересечения пополам, то
. Так как диагонали ромба делятся точкой пересечения пополам, то  .
.
По теореме Пифагора найдем АО и СО:
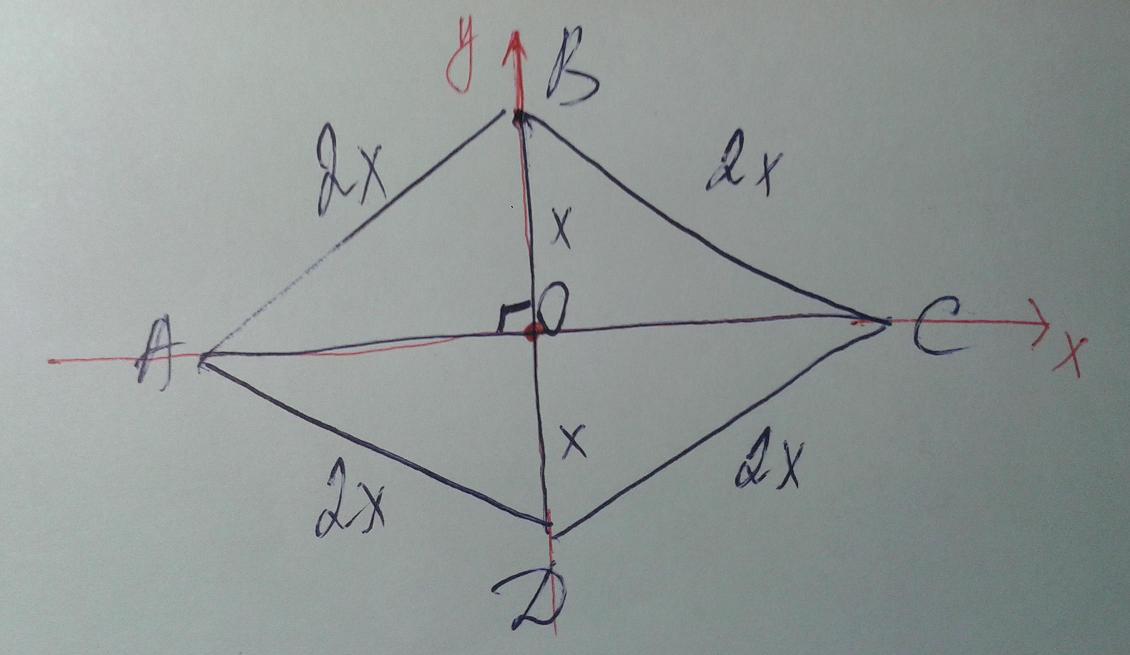
Введем систему координат с началом в точке О, причем, так как диагонали ромба пересекаются по прямым углом, ось х сонаправим с вектором ОС, а ось у сонаправим с вектором ОВ.
Находим координаты точек О, А, В, С,D:
О(0; 0); A(-x√3; 0); B(0; x); C(x√3; 0); D(0; -x)
Угол α между двумя векторами и
и  можно найти по формуле:
можно найти по формуле: 
а)
Каждая координата вектора высчитывается как разность между соответствующими координатами конца и начала вектора:

Или: воспользоваться тем что треугольник АВD равносторонний, а значит каждый его угол равен 60 градусов
б)

Или: воспользоваться тем что искомый угол можно найти как смежный с найденным в пункте а), а значит равный 180-60=120 градусов
в)

г)

Или: воспользоваться тем что диагонали ромба перпендикулярны, а значит искомый угол равен 90 градусов
д)

Или: воспользоваться тем что заданные векторы лежат на параллельных сторонах ромба, но направлены в противоположные стороны, значит угол равен 180 градусов
Тогда и диагональ
По теореме Пифагора найдем АО и СО:
Введем систему координат с началом в точке О, причем, так как диагонали ромба пересекаются по прямым углом, ось х сонаправим с вектором ОС, а ось у сонаправим с вектором ОВ.
Находим координаты точек О, А, В, С,D:
О(0; 0); A(-x√3; 0); B(0; x); C(x√3; 0); D(0; -x)
Угол α между двумя векторами
а)
Каждая координата вектора высчитывается как разность между соответствующими координатами конца и начала вектора:
Или: воспользоваться тем что треугольник АВD равносторонний, а значит каждый его угол равен 60 градусов
б)
Или: воспользоваться тем что искомый угол можно найти как смежный с найденным в пункте а), а значит равный 180-60=120 градусов
в)
г)
Или: воспользоваться тем что диагонали ромба перпендикулярны, а значит искомый угол равен 90 градусов
д)
Или: воспользоваться тем что заданные векторы лежат на параллельных сторонах ромба, но направлены в противоположные стороны, значит угол равен 180 градусов
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад