Question

Медиана прямоугольного треугольника , проведенная к гипотенузе, разбивает его на два треугольника с перимертами 16 см и 18 см. Найдите длины сторон треугольника

Answer 1

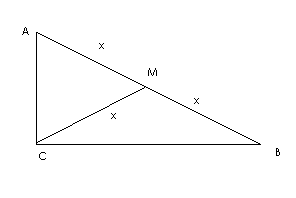
Cм. рисунок в приложении  

Свойство медианы прямоугольного треугольника:
ВМ=AM=MC
Обозначим ВМ=АМ=МС=х
Дано:
АВ+ВМ+AM=16    ⇒   AB = 16 - 2x
ВС+ВM+MC=18    ⇒   BC = 18 - 2x

По теореме Пифагора
АВ²+ВС²= AC²

(16-2х)²+(18-2х)²=(2х)²
256-64х+4х²+324-72х+4х²=4х²
4х²-136х+580=0
х²-34х+145=0
D=(-34)²-4·145=1156-580=576=24²

x=(34-24)/2=5     или      х=(34+24)/2=29
                                      не удовлетворяет
                                       условию задачи

АС=2х=10 см
АВ=16-10=6 см
ВС=18-10=8 см