Question

Отрезок CD пересекает плоскость бетта, точка Е - середина CD. Через точки С, D, Е проведены параллельные прямые, пересекающие плоскость бетта соотвественно в точках C1, D1 и Е1. Найдите ЕЕ1, если СС1 = 6/корень из 3 см и DD1 = корень из трех см.
Помогите, пожалуйста, должно получиться (корень 3)/2
Срочно!

Answer 1

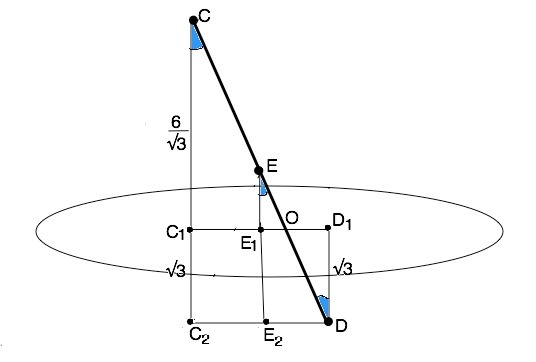
 По условию  СС₁║DD₁. Через две параллельные прямые можно провести плоскость, притом только одну. Отрезок СD  лежит в этой плоскости, С₁D₁- проекция  отрезка СD на плоскость β ⇒ С₁, Е₁ и D₁ лежат в на одной прямой.  

   Проведем через D параллельно C₁D₁ прямую до пересечения с продолжением СС₁  в т.С₂. Продолжим ЕЕ₁ до пересечения с DC₂  в точке Е₂.    Прямые C₁C₂║E₁E₂║D₁D;   C₂D₂║C₁D₁ ⇒ C₁C₂=E₁E₂=D₁D=√3. Домножив числитель и знаменатель значения СС₁ на √3, получим СС₁=2√3  Отрезок СС₂=СС₁+С₁С₂=2√3+√3=3√3 . Точка Е - середина CD, ЕЕ₂║СС2 ⇒ отрезок ЕЕ₂ - средняя линия треугольника СС₂D и равна половине СС₂. ЕЕ₂=3√3:2=1,5√3 Отсюда EE₁=ЕЕ₁-Е₁Е₁=1,5 √3-√3=0,5√3  или иначе ЕЕ₁=√3/2 см