Ответы
Ответ дал:
0
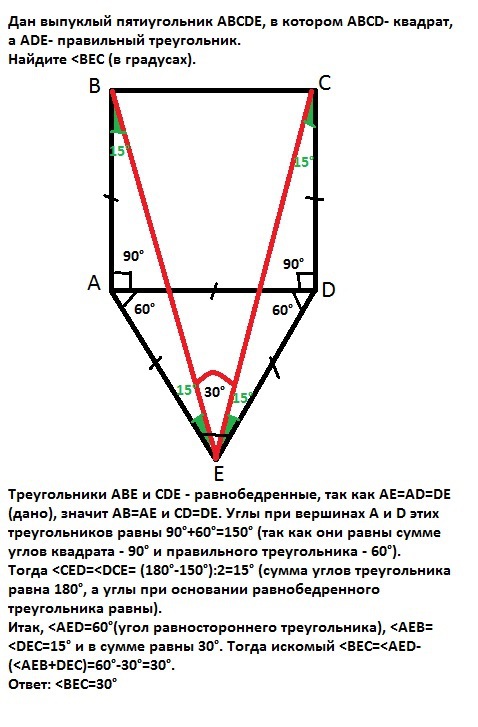
Треугольники АВЕ и СDE - равнобедренные, так как АЕ=АD=DE (дано), значит АВ=АЕ и CD=DE. Углы при вершинах А и D этих треугольников равны 90°+60°=150° (так как они равны сумме углов квадрата - 90° и правильного треугольника - 60°).
Тогда <CED=<DCE= (180°-150°):2=15° (сумма углов треугольника равна 180°, а углы при основании равнобедренного треугольника равны).
Итак, <AED=60°(угол равностороннего треугольника), <AEB=<DEC=15° и в сумме равны 30°. Тогда искомый <ВЕС=<AED-(<AEB+DEC)=60°-30°=30°.
Ответ: <ВЕС=30°
Тогда <CED=<DCE= (180°-150°):2=15° (сумма углов треугольника равна 180°, а углы при основании равнобедренного треугольника равны).
Итак, <AED=60°(угол равностороннего треугольника), <AEB=<DEC=15° и в сумме равны 30°. Тогда искомый <ВЕС=<AED-(<AEB+DEC)=60°-30°=30°.
Ответ: <ВЕС=30°
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
