Question

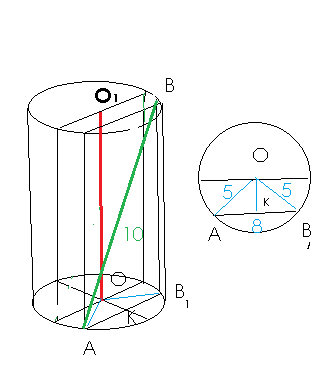
Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус основания равен 5 см, высота цилиндра равна 6 см, АВ=10 см. Определите расстояние между прямой АВ и осью цилиндра.

Answer 1

Проводим ВВ₁ || OO₁
Треугольник АВВ₁ - прямоугольный
АВ₁=8 ( по теореме Пифагора) или потому то это египетский треугольник
АВ₁²=АВ²-ВВ₁²=10²-6²=64=8²
Рассмотрим треугольник АОВ₁ ( см рисунок справа)
Равнобедренный треугольник. проведем высоту ОК.  По теореме Пифагора
ОК=3. 
Или потому что треугольник АОК - египетский
ОК- расстояние между плоскостью, содержащей отрезок АВ и плоскостью, содержащей ось ОО₁

Answer 2

СПАСИБО!