Question

8 класс. В треугольнике ABC AB = BC, AC = 4, высота BH равна 6 (точка H лежит на отрезке AC). Точка M - середина BC, точка К лежит на отрезке AC и угол MKC - прямой. Отрезки AM и BH пересекаются в точке Q. Найдите: а) длину отрезка MK б) величину угла AMK в) отношение AQ : AM

Answer 1

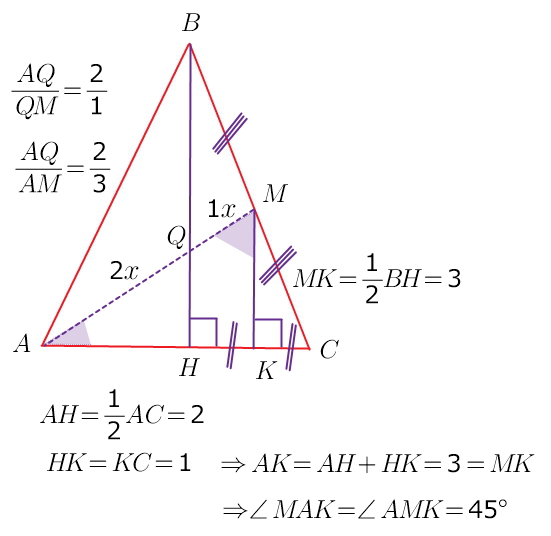
1. MK --средняя линия ΔВНС, т.к. MK || BH
средняя линия треугольника = половине стороны, к которой параллельна))
2. ВН--медиана (т.к. ΔАВС равнобедренный), К --середина НС (по п.1.))
---> ΔАКМ равнобедренный и прямоугольный, углы при основании по 45°
3. медианы треугольника точкой пересечения делятся в отношении 2:1,
считая от вершины... АМ тоже медиана... ее длина -- 3 части)))

Answer 2

в графическом редакторе...