Відношення основ рівнобічної трапеції 2:5.P=132 см.Обчислити середню лінію трапеції якщо її діагональ є бісектрисою гострого кута.
Отношение основ равносторонней трапеции 2: 5.P = 132 см.Обчислиты среднюю линию трапеции если ее диагональ является биссектрисой острого угла
Ответы
Ответ дал:
0
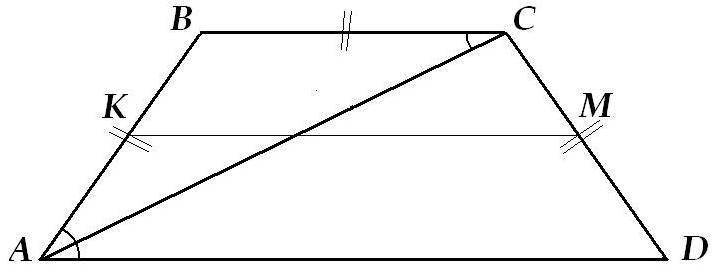
∠АСВ=∠CAD, как накрест лежащие при пересечении параллельных прямых секущей, значит ∠АСВ=∠САВ, т.к. АС - биссектриса по условию.
ΔАВС - равнобедренный, АВ=ВС=CD, т.к. трапеция равнобедренная по условию.
Обозначаем ,
, 

ΔАВС - равнобедренный, АВ=ВС=CD, т.к. трапеция равнобедренная по условию.
Обозначаем
Приложения:
Ответ дал:
0
спасибо огромное
Вас заинтересует
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад