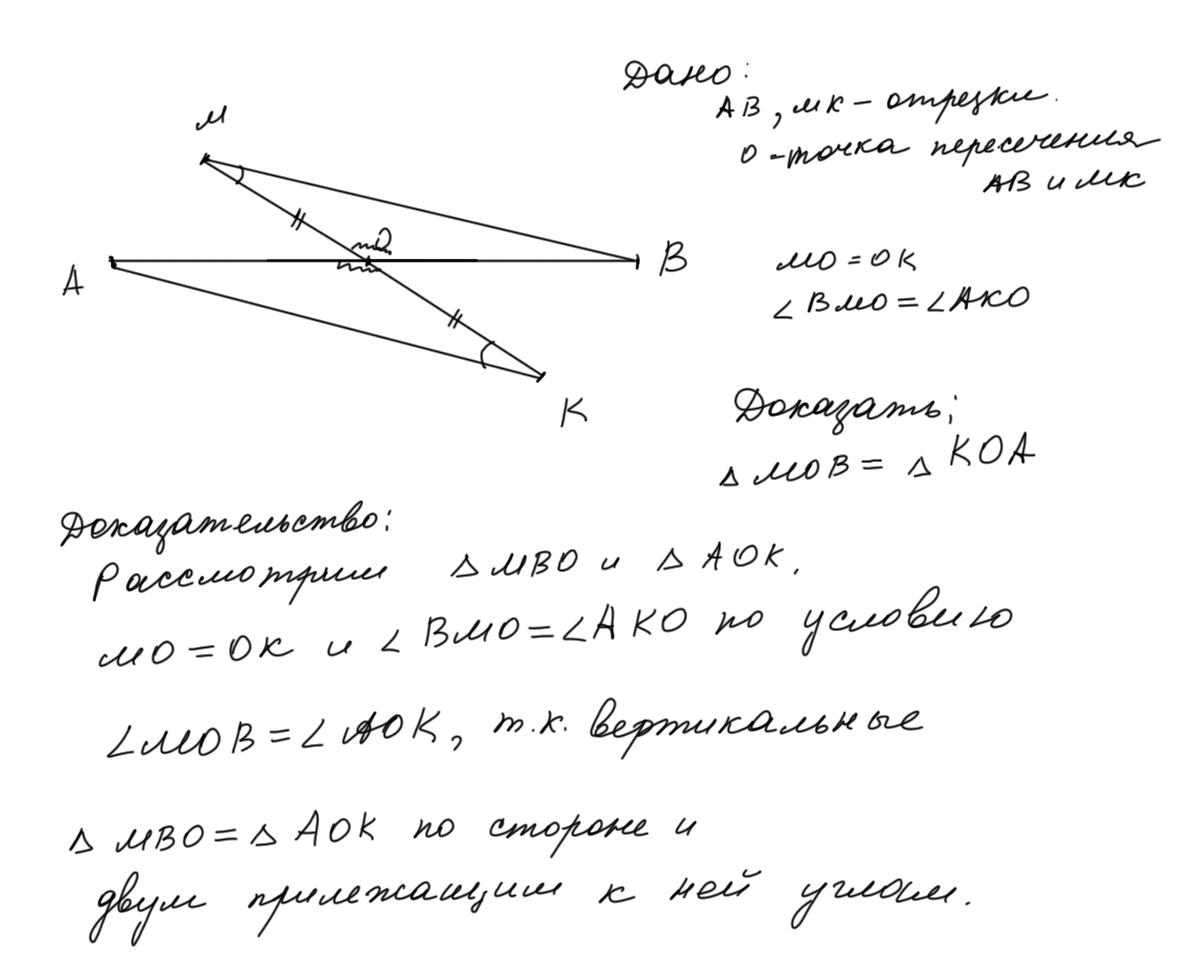
Отрезки AB и MK пересекаются в точке O, которая является серединой отрезка MK, ∠BMO = ∠AKO.
Докажите, что ΔMOB = ΔKOA.
Ответы
Ответ дал:
0
Решение в прикрепленном файле.
Приложения:
Ответ дал:
0
В треугольнике BMC стороны BM и MC равны, точка A лежит на биссектрисе MK.
Докажите, что AB = AC.
Докажите, что AB = AC.
Ответ дал:
0
Т.к. в треугольнике ВМС ВМ=МС, то он равнобедренный. МК - биссектриса, а также она является высотой, проведенной к основанию и медианой. МА - это серединный перпендикуляр к отрезку ВС. Все точки, лежащие на нем будут равноудалены от точек В и С. В том числе и точка А. Следовательно АВ=АС.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад