Question

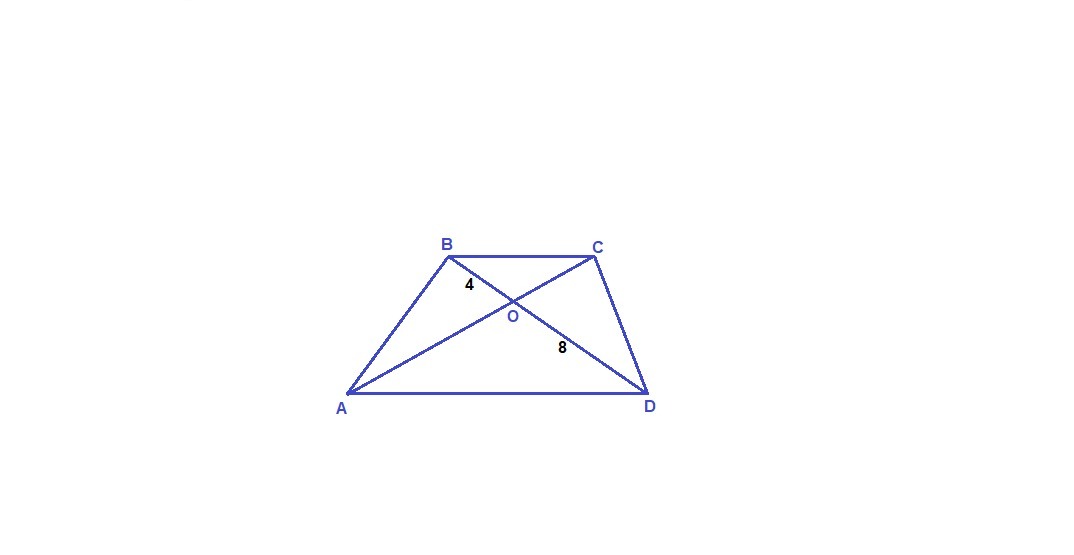
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. BO=4 см, OD=8 см, AC=15 см. Найдите длины OC и AO

Answer 1

∠СВО = ∠ADO как накрест лежащие при пересечении ВС ║ AD секущей BD,

∠ВОС = ∠DOA как вертикальные, значит

ΔВОС подобен ΔDOA по двум углам.

CO : AO = BO : OD = 4 : 8 = 1 : 2

Значит, АО = 2СО,    

АС = АО + СО = 15

2СО + СО = 15

3СО = 15

СО = 5 см

АО = 2 · 5 = 10 см