Question

найдите площадь фигуры ограниченной линиями y=$sqrt{x}$, y=x-6, y=0
Или в приложении

Answer 1

**********************

Answer 2

где не понятно - поясню

Answer 3

все понятно! спасибо огромное !!!

Answer 4

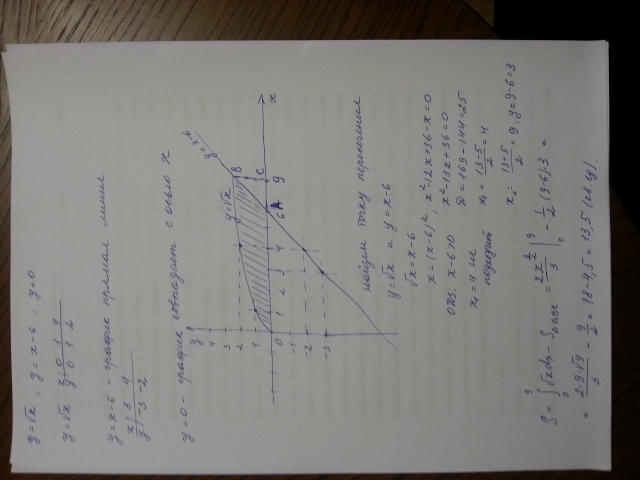
найдем пределы интегрирования
√х=х-6
х≥6
х=х²-12х+36
х²-13х+36=0
х1+х2=13 и х1*х2=36
х1=4 и х2=9
На промежутке от 0 до 6 фигура ограничена сверху графиком у=√х и осью ох снизу , а на промежутке от 4 до 6 сверху у=√ч и снизу у=х-6.
$S= intlimits^6_0 { sqrt{x} } , dx + intlimits^9_6 {( sqrt{x} -x+6)} , dx =$$2/3*6 sqrt{6} +2/3*9*3-40,5+54-2/3*6 sqrt{6} +18-36=18-40,5$$+54+18-36=13,5$

Answer 5

На промежутке от 4 до 6 фигура ограничена сверху графиком у=√х и осью ох

Answer 6

Учла,что ограничена