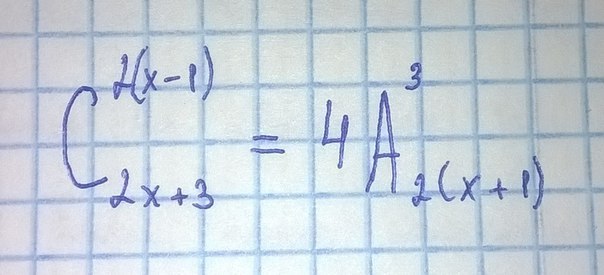Ответы
Ответ дал:
0
Формулы:



(2x-1)· 2x· (2x+1)· (2x+2)· (2x+3)-120·2x· (2x+1) ·(2x+2)=0
2x· (2x+1)· (2x+2)·((2x-1)(2x+3)-120)=0
2x=0 или 2x+1=0 или 2x+2=0 или (2x-1)(2x+3)-120=0
х₁=0 х₂=-0,5 х₃=-1 4х²+4х-123=0
D=4²-4·4·(-123)=4²(1+123)=4²·124
x₄=(-4-8√31)/8 или х₅=(-4+8√31)/8
(2x-1)· 2x· (2x+1)· (2x+2)· (2x+3)-120·2x· (2x+1) ·(2x+2)=0
2x· (2x+1)· (2x+2)·((2x-1)(2x+3)-120)=0
2x=0 или 2x+1=0 или 2x+2=0 или (2x-1)(2x+3)-120=0
х₁=0 х₂=-0,5 х₃=-1 4х²+4х-123=0
D=4²-4·4·(-123)=4²(1+123)=4²·124
x₄=(-4-8√31)/8 или х₅=(-4+8√31)/8
Ответ дал:
0
Это 5!=1*2*3*4*5=120
Ответ дал:
0
А как берутся факториалы от таких значений как (2х+2)!
Ответ дал:
0
Это произведение всех чисел от 1 до (2х+2) ; (2х+2)!=1*2*3*... (2х-1)*2х*(2х+1)(2х+2)
Ответ дал:
0
Поэтому это произведение можно сократить на (2х-1)! Останется 2х*(2х+1)(2х+2)
Ответ дал:
0
А еще пожалуйста объясните, с дискриминантом что-то не понимаю, как получилось, что 4^2 * (1+123)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад