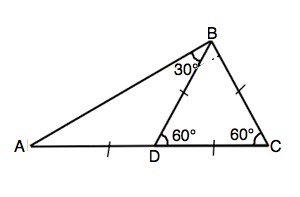
В треугольнике ABC угол c=60 градусам. На стороне AC отмечена точка D так, что угол BDC=60 градусов, угол ABD=30 градусам. а) Докажите, что AD=BC б) Докажите, что периметр треугольника ABC меньше пяти длин отрезка BC
Ответы
Ответ дал:
0
В ∆ ВDC два угла по 60° (дано) ⇒
∠DBC=180°-2•60°=60°⇒
∆ BDC - равносторонний.
BD=BC=DC
В ∆ АВС угол АВС=∠ABD+∠CBD=30°+60°=90° ⇒
∠ВАС=180°-(90°+60°)=30°
Углы при АВ в ∆ ADB равны, ⇒ он равнобедренный.
АD=BD=BC ⇒
AC=2•BC
P(ABC)=AB+2BC+BC
Из ∆ ABD сторона АВ < AD+BD (неравенство треугольника).⇒
АВ < 2ВС⇒
Р(АВС) меньше 5 ВС
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад