Question

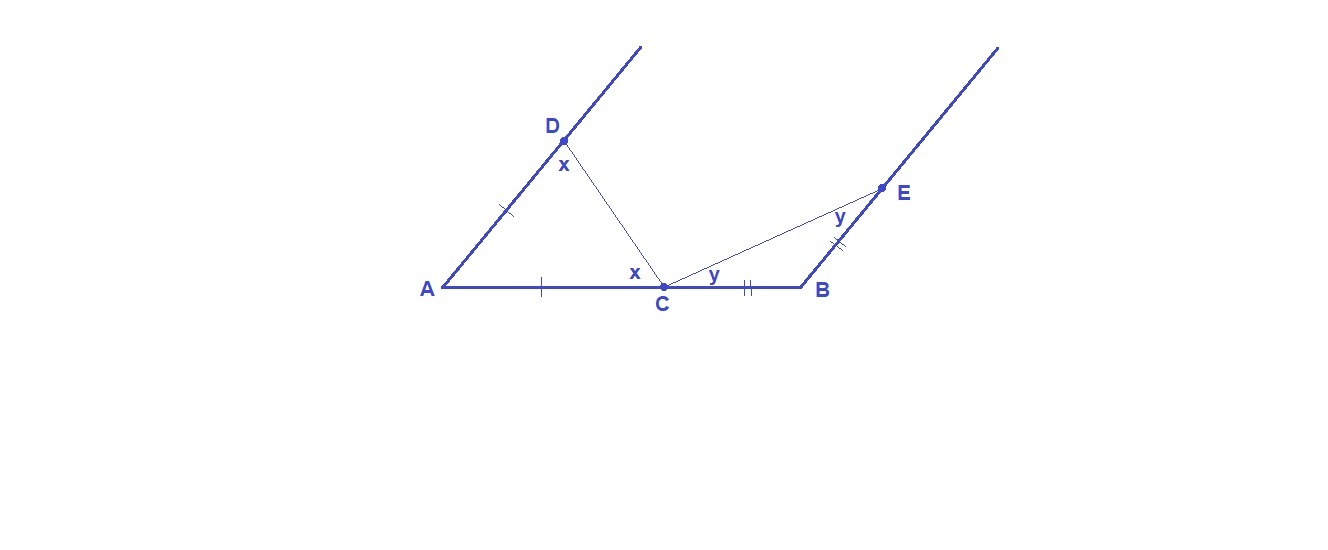
На отрезке AB взята точка C. Через точки A и B проведены по одну сторону от AB параллельные лучи. На них отложены отрезки AD=AC и BE=BC. Точка C
соединена отрезками прямых с точками D и E. Докажите, что dc перп. ce

Answer 1

По условию ΔADC равнобедренный с основанием CD, значит углы при основании равны, обозначим их х.

ΔВЕС так же равнобедренный с основанием СЕ, значит углы при основании равны, обозначим их у.

Сумма углов треугольника равна 180°, значит

∠А = 180° - 2х

∠В = 180° - 2у

∠А + ∠В = 180°, так как он односторонние при пересечении параллельных прямых AD и ВЕ секущей АВ. Тогда

(180° - 2x) + (180° - 2y) = 180°

2x + 2y = 180°

x + y = 90°

Угол АСВ развернутый, равен 180°.

∠DEC = 180° - (х + у) = 180° - 90° = 90°

Значит DC⊥CE