вычислить площадь фигуры ограниченной линиями
у=1/х2
у=1
х=-3
х=-2
пожалуйста, помогите очень нужно (желательно с вложением, чтобы таблица, рисунок, интегралы - всё было) очень нужно
Ответы
Ответ дал:
0
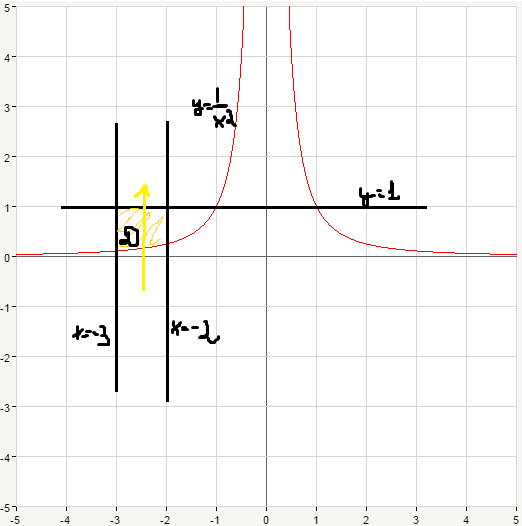
Делаем рисунок(во вложении).
Находим пределы интегрирования по х и у(для перехода к повторному).
Как видно х изменяется от -3 до -2.
Для у проводим стрелку снизу вверх и смотрим через что она входит в фигуру и выходит. Входит через y=1/x², выходит через y=1.
Нашли пределы, осталось вычислить интеграл:

Находим пределы интегрирования по х и у(для перехода к повторному).
Как видно х изменяется от -3 до -2.
Для у проводим стрелку снизу вверх и смотрим через что она входит в фигуру и выходит. Входит через y=1/x², выходит через y=1.
Нашли пределы, осталось вычислить интеграл:
Приложения:
Ответ дал:
0
спасибо, но можете объяснить. я не поняла как 2 интеграла в одном. можно их как то разделить. мы всегда по отдельности делали
Ответ дал:
0
можете показать как вы делали?
Ответ дал:
0
мы сначала находили большой интеграл потом маленький а потом отнимали
Ответ дал:
0
но нам сказали что это легкий . в одно действие вроде
Ответ дал:
0
Не нужно никаких двойных интегралов.
Alabaster рисунок нарисовал правильно, а с интегралом намудрил.

Alabaster рисунок нарисовал правильно, а с интегралом намудрил.
Приложения:

Ответ дал:
0
Спасибо большое)
Ответ дал:
0
никто не говорил что нельзя использовать двойной интеграл
Ответ дал:
0
Можно, конечно, но в школе его не проходят, а это явно школьница спрашивает.
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад