Геометрия срочно
А1 Какая из перечисленных точек лежит в YOZ:
а) А(0;1;1); в) С(-1;0;5);
б) В(1;2;0); г) D(1;1;2);
А2 Точка М – середина отрезка АВ. Найдите координаты точки В, если А(1;3; -2), М( -2;4;5).
а) В( -5;5;12); в) В( -2;5;2);
б) В(3;5;8); г) другой ответ.
А3 Найдите длину АМ – медианы треугольника АВС,
Если А(1;2;3), В(6;3;6), С(-2;5;2)
а) ; в) 3;
б) 2; г) другой ответ.
А4 Найдите скалярное произведение векторов
а (1,-1,2) в (-1,1,1)
а) -3 б) 0 в) 1 г) 2
А5 Найдите координаты точек, в которые переходит точки А (0,1,2) В (3,-1,4) с (-1,0,-2) при
симметрии относительно оси 0Х.
а) б) в) г)
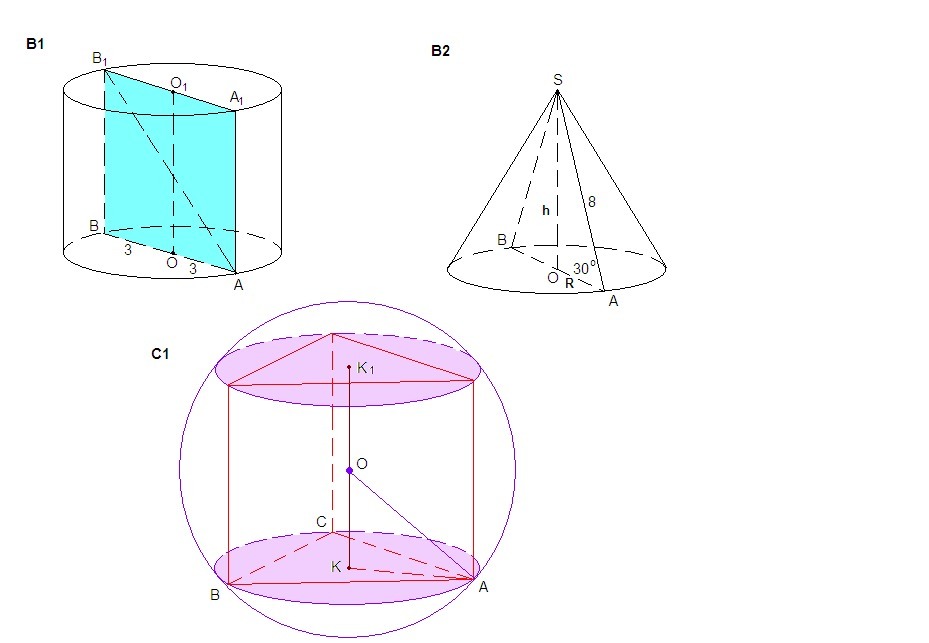
В1 Диагональ осевого сечения цилиндра равна см, а радиус основания – 3 см. Найдите
высоту цилиндра.
Ответ___________________________
В2 Образующая конуса наклонена к плоскости основания под углом 30° и равна 8 см. Найдите
площадь осевого сечения конуса.
Ответ___________________________
С1 Правильная треугольная призма вписана в шар. Найдите высоту призмы, если радиус шара 4
см, а ребро основания призмы – 6 см
Ответы
А1 Если точка лежит в плоскости YOZ, то x=0;
Ответ: а) A(0; 1; 1).
A2 Координаты середины отрезка равны полусумме координат концов отрезка:
x(М) = (x(A) + x(В))/2; ⇒ x(B)=2· x(M) - x(A);
x(B) = 2 · (- 2) - 1 = - 5
y(B) = 2 · 4 - 3 = 5
z(B) = 2 · 5 - (- 2) = 12
Ответ: a) B(- 5; 5; 12).
A3 B(6; 3; 6) C(- 2; 5; 2)
Если АМ медиана, то M - середина ВС.
x(M) = (6 - 2)/2 = 2; y(M) = (3 + 5)/2 = 4; z(M) = (6 + 2)/2 = 4
M(2; 4; 4); A(1; 2; 3)
AM² = (2 - 1)² + (4 - 2)² + (4 - 3)² = 1 + 4 + 1 = 6;
AM = √6
Ответ: а) √6
А4 Скалярное произведение равно сумме произведений соответствующих координат:
↑a · ↑b = 1 · (- 1) + (- 1) · 1 + 2 · 1 = - 1 - 1 + 2 = 0
Ответ: б) 0.
А5 При симметрии относительно оси Ох меняют знак координаты у и z:
А(0; 1; 2) → A₁ (0; - 1; - 2),
B(3; - 1; 4) → B₁ (3; 1; - 4),
C(- 1; 0; - 2) → C₁ (- 1; 0; 2).
B1 Неполное условие. Должно быть так:
Диагональ осевого сечения цилиндра равна √81 см, а радиус основания – 3 см. Найти высоту цилиндра.
Осевое сечение цилиндра - прямоугольник, одна сторона которого (АВ) равна диаметру основания, а другая - образующая (она же высота).
Из прямоугольного треугольника АВВ₁ по теореме Пифагора:
ВВ₁ = √(АВ₁² - АВ²) = √(81 - 36) = √45 = 3√5 см
Ответ: 3√5 см
B2 ΔSOA прямоугольный,
R = OA = SA · cos30° = 8 · cos30° = 8 √3/2 = 4√3 см
h = SO = SA · sin30° = 8 · 1/2 = 4 см
Sasb = 1/2 AB · SO = 1/2 · 2R · h = R · h = 4√3 · 4 = 16√3 см²
С1 Если призма вписана в шар, то ее основания вписаны в равные круги - параллельные сечения шара, а центр шара - точка О - лежит на середине отрезка КК₁, соединяющего центры этих кругов.
Отрезок, соединяющий центр шара с центром сечения, перпендикулярен сечению. ОК перпендикулярен плоскости АВС. Тогда КК₁ - высота призмы.
ОА - радиус шара, ОА = 4 см,
КА - радиус сечения, или радиус окружности, описанной около правильного треугольника АВС (призма правильная), тогда
КА = а√3/3, где а - ребро осноавния,
КА = 6√3/3 = 2√3 см
Из прямоугольного треугольника АОК по теореме Пифагора:
ОК = √(ОА² - КА²) = √(4² - (2√3)²) = √(16 - 12) = √4 = 2 см
КК₁ = 2ОК = 4 см
Ответ: 4 см