Question

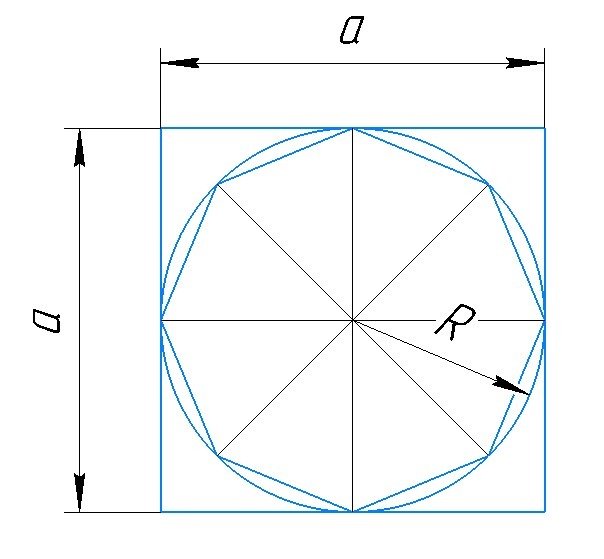
В квадрат, площадь которого равна 25см2, вписана окружность. Определите площадь правильного восьмиугольника, вписанного в эту окружность.

Answer 1

Найдем строну квадрата
 
$a = sqrt{S} = sqrt{25} = 5$  см

Если из центра восьмиугольника провести отрезки соединяющие вершины, то вписанный многоугольник будет разбит на восемь одинаковых равнобедренных треугольников. Боковая торона которых будет равна радиусу описанной окружности или половине диаметра.

$R = frac{a}{2} = frac{5}{2}$ см

Учитывая, что отрезки делят окружность на 8 равных частей, то угол при вершине будет равен
$frac{360^0}{8} = 45^0$

Найдем прощать такого треугольника через стороны и угол между ними
$S = frac{1}{2} *R * R * sin 45^0 = frac{1}{2} * frac{5}{2} * frac{5}{2} * frac{ sqrt{2} }{2} = frac{ 25sqrt{2} }{16}$

Площадь восьмиугольника в 8 раз больше площади треугольника

$S_8 = 8* frac{ 25sqrt{2} }{16} = 12,5sqrt{2} approx 17,68 cm^2$

Ответ: 
$S = 12,5sqrt{2} approx 17,68 cm^2$