Question

Помогите, пожалуйста (:
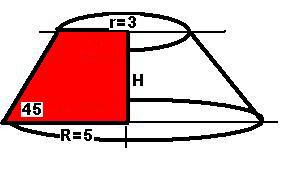
Прямоугольная трапеция с углом 45 градусов вращается вокруг прямой, содержащей меньшую боковую сторону. Найдите площадь поверхности тела вращения, если основания трапеции равны 3 и 5.

Answer 1

Эта трапеция превращается в усеченный конус с радиусами оснований 3 и 5.
Высоту вычисляем. как второй катет равнобедренного треугольника.
Один катет равен R-r = 5-3=2 =H - высота трапеции.
Площадь ДВУХ  оснований Sосн = пи*(R^2+r^2) = 34*пи = 106,8 кв.см
Боковая поверхность 
Sбок = пи*(R-r)*L - где L - образующая.
Образующую вычислим по т. Пифагора
L^2 = 8   L~ 2.83
Подставляем и вычисляем
Sбок = 3,14*2*2,83 = 50,3 кв.см.
Полная поверхность = 157,1 кв.см.
Ответ% 157,1 или 50,3 + 106,8

Answer 2

Огромное спасибо!