Question

Построить график функции y = 2*∛(x²) * e^(-x/3) по следующему алгоритму:
1) Область определения функции
2) Непрерывность функции и её четность(lim y =? при x-> +- ∞)
3) Пересечение с осями координат и точки разрыва (найти точки разрыва с помощью пределов)
4) Асимптоты (вертикальные и наклонные, найти их через пределы)
5) Возрастание, убывание, экстремумы функции(через достаточные условия)
6) Выпуклость, вогнутость и перегибы графика
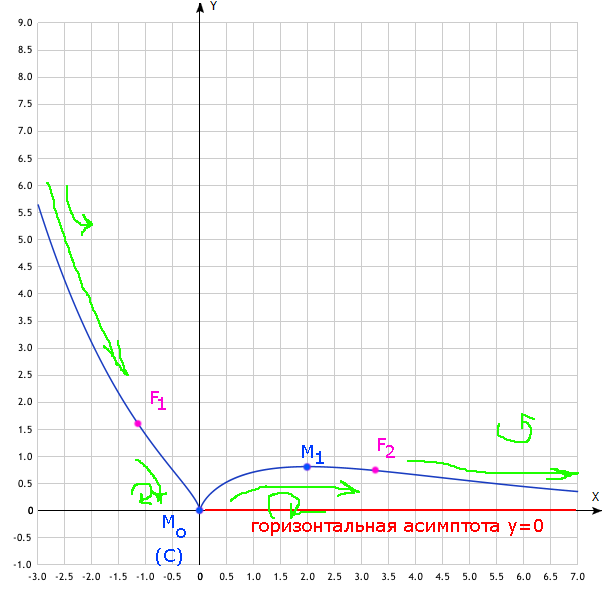
7) Построить сам график со всеми асимптотами

Answer 1

Дано:
$y = sqrt[3]{x^2} e^{ -frac{x}{3} }$ ;

Исследовать функцию и построить график.


Решение:

1) Функция определена при любых аргументах.

D(f) ≡ R ≡ $( -infty ; +infty )$ ;



2) Функция не является ни чётной, ни нечётной. Докажем это:

$y(-x) = sqrt[3]{ (-x)^2 } e^{ -frac{-x}{3} } = sqrt[3]{ x^2 } e^{ frac{x}{3} }$ ;

$y(-x)/y(x) = frac{ sqrt[3]{ x^2 } exp{ frac{x}{3} } }{ sqrt[3]{ x^2 } exp{ ( -frac{x}{3} ) } } = frac{ exp{ frac{x}{3} } }{ exp{ -frac{x}{3} } } = exp{ frac{x}{3} } exp{ frac{x}{3} } = exp{ frac{2x}{3} }$ ≠ ± 1 при любых аргументах ;

$y(-x)/y(x)$ ≠ ± 1 ;


Найдём первую производную функции y(x) :

$y'(x) = ( sqrt[3]{x^2} e^{ -frac{x}{3} } )' = ( x^frac{2}{3} e^{ -frac{x}{3} } )' = frac{2}{3} x^{ -frac{1}{3} } e^{ -frac{x}{3} } + x^frac{2}{3} ( -frac{1}{3} ) e^{ -frac{x}{3} } =$

$= frac{ e^{ -frac{x}{3} } }{3} ( frac{2}{x^frac{1}{3} } - x^frac{2}{3} ) = frac{ e^{ -frac{x}{3} } }{ 3 x^{1/3} } ( 2 - x )$ ;

$y'(x) = frac{ e^{ -frac{x}{3} } }{ 3 sqrt[3]{x} } ( 2 - x )$ ;


При x = 0, производная y'(x) – не определена, хотя сама функция определена при любых аргументах, так что функция непрерывна на всей числовой прямой, но непрерывно-дифференцируема за исключением ноля.

Убедимся в этом, вычислив предел около ноля слева и справа

$lim_{x to -0} y(x) = lim_{x to -0} sqrt[3]{x^2} e^{ frac{x}{3} } = sqrt[3]{ (-0)^2 } e^{ -frac{-0}{3} } = sqrt[3]{0} e^{0} = 0*1 = 0$ ;

$lim_{x to +0} y(x) = lim_{x to +0} sqrt[3]{x^2} e^{ frac{x}{3} } = sqrt[3]{ (+0)^2 } e^{ -frac{0}{3} } = sqrt[3]{0} e^{0} = 0*1 = 0$ ;



3) Функция определена при любых x, поэтому точек разрыва нет.


Если приравнять функцию к нолю, получим:

$y(x) = 0$ ;

$sqrt[3]{x^2} e^{ frac{x}{3} } = 0$ ;

Что возможно только при $sqrt[3]{x^2} = 0$ , т.е. при x = 0 ;

Итак, точка ( 0 ; 0 ) – принадлежит нашему графику.




4. Найдем асимптоты y(x).

Точек разрыва нет, значит, нет и вертикальных асимптот.

Посмотрим, что происходит с функцией y(x) при устремлении аргумента к ± $infty$ :

$lim_{x to -infty} y(x) = lim_{x to -infty} sqrt[3]{x^2} e^{ -frac{x}{3} } = lim_{x to -infty} e^{ ln{ sqrt[3]{x^2} } } e^{ -frac{x}{3} } =$

$= lim_{x to -infty} e^{ frac{2}{3} ln{ (-x) } } e^{ frac{-x}{3} } = lim_{x to -infty} e^{ frac{2}{3} ln{ (-x) } + frac{-x}{3} } =$

$= lim_{x to -infty} e^{ frac{-x}{3} ( 1 + frac{ 2 ln{ (-x) } }{ -x } ) } > lim_{x to -infty} e^{ frac{-x}{3} } = +infty$ ;


$lim_{x to -infty} y(x) = +infty$ ;



$lim_{x to +infty} y(x) = lim_{x to +infty} sqrt[3]{x^2} e^{ -frac{x}{3} } = lim_{x to +infty} e^{ ln{ sqrt[3]{x^2} } } e^{ -frac{x}{3} } =$

$= lim_{x to +infty} e^{ frac{2}{3} ln{x} } e^{ -frac{x}{3} } = lim_{x to +infty} e^{ frac{2}{3} ln{x} - frac{x}{3} } =$

$= lim_{x to +infty} e^{ -frac{x}{3} ( 1 - frac{ 2 ln{x} }{x} ) } < lim_{x to +infty} e^{ -frac{x}{3} } leq 0$ ;


Поскольку, $lim_{x to +infty} y(x) geq 0$ , то:

$lim_{x to +infty} y(x) = 0$ ;

Значит, уходя на отрицательную бесконечность аргумента y(x) и сама стремиться к бесконечности, а уходя на положительную бесконечно по аргументу y(x) стремится к нулю ;

Из этого следует, что при x>0 есть горизонтальная асимптота y = 0 .

Чтобы найти наклонную асимптоту, найдем предел первой производной на отрицательной бесконечности по аргументу:

$lim_{x to -infty} y'(x) = lim_{x to -infty} frac{ e^{ -frac{x}{3} } }{ 3 sqrt[3]{x} } ( 2 - x ) > lim_{x to -infty} frac{ e^{ -frac{x}{3} } }{ 3 sqrt[3]{x} } ( - x )$ ;

$lim_{x to -infty} frac{ e^{ -frac{x}{3} } }{ 3 sqrt[3]{x} } ( - x ) = lim_{x to -infty} ( -frac{1}{3} sqrt[3]{x^2} e^{ -frac{x}{3} } ) = -infty$ – по доказанному в пределе самой функции .

$lim_{x to -infty} y'(x) = -infty$ ;

А это означает, что наклонной асимптоты на отрицательной бесконечности нет. А на положительной – горизонтальная.

Answer 2

Готово. Сейчас ещё проверю одним глазком.